HA & HB Loading Example
BS 5400 Part 2 : 2006 Clause 6.2 Type HA Loading
Problem:
How do you work out the HA loading and bending moment for a bridge deck ?
Example:
Carriageway = 6m wide
Deck span = 34m (centre to centre of bearings for a simply supported single span)
Design for a metre width of deck :
Cl 3.2.9.3.1.
Number of notional lanes = 2
Notional lane width = 6.0/2 = 3.0m
Cl 6.2.1.
Loaded length = 34m
W = 336(1/L)0.67 kN/m (per notional lane)
W = 31.6 kN/m (per notional lane)
Cl 6.2.2.
Knife Edge Load = 120 kN (per notional lane)
Cl 6.4.1.1. Table 14.
α2 = 0.0137[bL(40-L)+3.65(L-20)]
α2 = 0.0137[3.0(40-34.0)+3.65(34.0-20)] = 0.947
Note: For loaded lengths less than 20m the load is proportioned to a standard lane width of 3.65m, i.e. 0.274bL = bL/3.65.
For a metre width of deck :
W = (31.6 x 0.947)/3.0 = 10.0 kN/m
KEL = (120 x 0.947)/3.0 = 37.88 kN
Maximum mid span Bending Moment with KEL at mid span:
M = (10.0 x 342)/8 + (37.88 x 34)/4 = 1767 kNm
Cl 6.2.7.
γfL = 1.20 (Serviceability limit state - combination 1)
γfL = 1.50 (Ultimate limit state - combination 1)
Design HA moment for a metre width of deck :
Msls = 1767 x 1.2 = 2120 kNm
Mult = 1767 x 1.5 = 2650 kNm
Note: Use of γf3
BS 5400 Pt.3 & Pt.5 - γf3 is used with the design strength so
Mult = 2650 kNm.
BS 5400 Pt.4 - γf3 is used with the load effect so
Mult = 1.1 x 2650 = 2915 kNm.
Assume the road over the bridge is not a Principal Road then we need to check for 30 units type HB loading (see BD 37/01 Chapter 4).
Cl 6.3.1
Nominal load per axle = 30units x 10kN = 300kN
The maximum bending moment will be achieved
by using the shortest HB vehicle i.e. with 6m spacing (see BS 5400-2:2006 Fig 12).
The maximum moment for a simply supported span occurs under the inner axle
when the vehicle is positioned such that the mid span bisects the distance
between the centroid of the load and the nearest axle.
With a 34m span and the 6m HB vehicle with equal axle loads, the inner axle
is placed at 1.5m from the mid span.
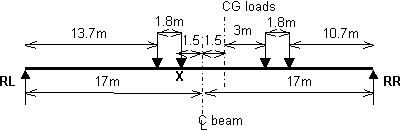
RL = 300(10.7+12.5+18.5+20.3)/34 = 547 kN
RR = 4x300-547 = 653kN
Moment at X = 547x15.5 - 300x1.8 = 7939kNm
Cl 6.4.2
The HB vehicle occupies one lane with HA load in the adjacent lane. Assume for the example that the HB load is carried by a standard lane width of 3.65m.
Hence the moment per metre width of deck = 7939/3.65 = 2175kNm
Cl 6.3.4.
γfL =
1.10 (Serviceability limit state - combination 1)
γfL =
1.30 (Ultimate limit state - combination 1)
Design HB moment for a metre width of deck :
Msls = 1.1 x 2175 = 2393 kN/m (compared to 2120 for HA
load)
Mult = 1.3 x 2175 = 2828 kN/m (compared to 2650 for HA
load)
Hence in this case HB load effects would govern although a grillage or
finite element type distribution would reduce the HB moment considerably.
Contact David Childs