Reinforced Concrete Deck Example to British Standards
Reinforced Concrete Deck Design to BS 5400 Part 4
Problem:
Design a simply supported reinforced concrete deck slab using a unit strip method.
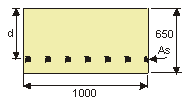
The deck carries a 100mm depth of surfacing,
together with a nominal HA live load udl of 17.5 kN/m2 and knife edge load of 33kN/m .
The deck should also be designed to
carry 30 units of HB load. The span of the deck is 12.0m centre to centre of bearings.
γconc. = 25kN/m3
30 units of HB also to be considered.
Use C32/40 concrete to BS 8500.
Use Grade B500B reinforcement to BS 4449.
BS 8500-1 cl. A.2.1 Table A.1
Exposure Class XD1 used for bridge deck soffits.
cl. A.3
Fixing tolerence for reinforcement Δc = 15mm for insitu concrete.
Table A.5
Nominal cover for C32/40 concrete = 45 + Δc = 60mm with
maximum water-cement ratio = 0.55 and minimum cement content of 320 kg/m3
Loading per metre width of deck (unit strip)
(Note: The loading has been simplified to demonstrate the method of designing the slab (See BS 5400 Pt2, or BD 37/01 for full design loading).
Nominal Dead Loads :
deck slab = 25 × 0.65 × 1.0 = 16.3 kN/m
surfacing = 24 × 0.1 × 1.0 = 2.4 kN/m
Nominal Live Load :
HA = 17.5 × 1.0 + 33.0 = 17.5 kN/m(udl) + 33kN(kel)
30 units HB = 30 × 10 / 4 per wheel = 75 kN per wheel
Load factors for serviceability and ultimate limit state from BS 5400 Part 2 Table 1:
SLS
ULS
Comb 1
Comb 3
Comb 1
Comb 3
Dead Load
γfL concrete
1.0
1.0
1.15
1.15
Superimposed Dead Load
γfL surfacing
1.2
1.2
1.75
1.75
Live Load
γfL HA
1.2
1.0
1.5
1.25
γfL HB
1.1
1.0
1.3
1.1
Temperature Difference
γfL
—
0.8
—
1.0#
Key: # It is usually assumed that there is local plasticity at the critical sections at Ultimate Limit State and the self equilibrating stresses due to non linear temperature distribution can be ignored in combination loadings. (Ref:"Concrete bridge engineering:performance and advances" by R.J.Cope).
Temperature Difference Effects
Apply temperature differences given in BS 5400 Pt2 Fig.9 (Group 4) to a 1m wide deck section.
Cl. 5.4.6 - Coefficient of thermal expansion = 12 × 10-6 per °C.
From BS 5400 Pt4 Table 3 : Ec = 31 kN/mm2 for fcu = 40N/mm2
Hence restrained temperature stresses per °C = 31 × 103 × 12 × 10-6 = 0.372 N/mm2
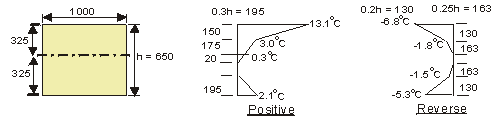
Section Properties
Area = 1000 × 650 = 0.65 × 106 mm2
Second Moment of Area = 1000 × 6503 / 12 = 22.9 × 109 mm4
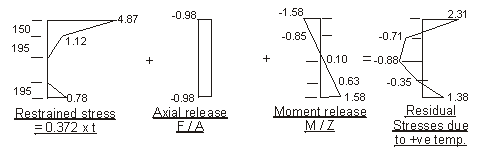
a) Positive temperature difference
Force F to restrain temperature strain :
0.372 × 103 × [ 150 × ( 3.0 + 5.05 ) + (195 × 1.5) + (195 × 1.05)] × 10-3 = 634.2 kN
Taking moments about centroid of section to determine required moment M to restrain
curvature due to temperature strain :
0.372 × 103 × [150 × (3.0 × 250 + 5.05 × 275) + 175 × (0.3 × 87.5 + 1.35 × 116.7) - (20 × 0.15 × 6.7) - (195 × 1.05 × 260)] × 10-6 = 111.5kNm
b) Reverse temperature difference
Force F to restrain temperature strain :
- 0.372 × 103 × [ 130 × ( 1.8 + 2.5 + 1.5 + 1.9 ) + 163 × ( 0.9 + 0.75 )] × 10-3 = - 472.4kN
Taking moments about centroid of section to determine required moment M to restrain
curvature due to temperature strain :
- 0.372 × 103 × [130 × ( 1.8 × 260 + 2.5 × 282 - 1.5 × 260 - 1.9 × 282 ) + 163 × ( 0.9 × 141 - 0.75 × 141 )] × 10-6 = -13.34kNm
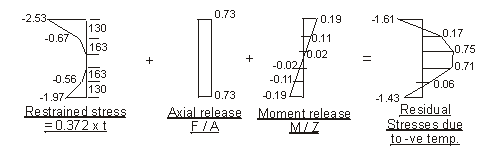
Note: Sign convention is compressive stresses are positive.
Dead + Superimposed Dead Loading (per metre width of deck)
SLS = Serviceability Limit State
ULS = Ultimate Limit State
Design SLS moment = ∑(γfL × M) = [(1.0 × 16.3)+(1.2 × 2.4)] × 122 / 8 = 345 kNm
Design ULS moment = γf3 × ∑(γfL × M) = 1.1 × [{(1.15 × 16.3)+(1.75 × 2.4)} × 122 / 8] = 454 kNm
Live Loading (per metre width of deck)
Nominal HA mid span moment = 17.5 × 12.02 / 8 + 33.0 × 12.0 / 4 = 414kNm
The maximum moment for the HB vehicle occurs at point X in the diagram below with the vehicle positioned as shown.
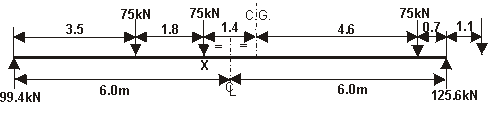
(CG = position of the centre of gravity of the three 75kN wheel loads)
Nominal HB moment at X = 99.4 × 5.3 - 75 × 1.8 = 392kNm
Combination 1 Loading
Design HA SLS moment = γfL × M = 1.2 × 414 = 497 kNm
Design HB SLS moment = γfL × M = 1.1 × 392 = 431 kNm < 497 kNm ∴ HA critical
Total Design SLS Moment (Dead + Live) = 345 + 497 = 842 kNm
Design HA ULS moment = γf3 × γfL × M = 1.1 × 1.5 × 414 = 683 kNm
Design HB ULS moment = γf3 × γfL × M = 1.1 × 1.3 × 392 = 561 kNm < 683 kNm
∴ HA loading critical
Total Design ULS Moment (Dead + Live) = 454 + 683 = 1137 kNm
Combination 3 Loading
Design HA SLS moment = γfL × M = 1.0 × 414 = 414 kNm
Design HB SLS moment = γfL × M = 1.0 × 392 = 392 kNm <414 kNm ∴ HA loading critical
Design SLS Moment (Dead + Live) = 345 + 414 = 759 kNm
Design HA ULS moment = γf3 × γfL × M = 1.1 × 1.25 × 414 = 569 kNm
Design HB ULS moment = γf3 × γfL × M = 1.1 × 1.1 × 392 = 474 kNm < 569 kNm
∴ HA loading critical
Design ULS Moment (Dead + Live) = 454 + 569 = 1023 kNm
BS 5400 Pt 4 cl. 5.1.2.1
It is usual to design reinforced concrete for the ultimate limit state and check for serviceability conditions.
cl. 5.4.2
Use clause 5.3.2 for the resistance moments in slabs.
cl. 5.3.2.3
Try 32mm dia. reinforcement at 125mm centres:
Nominal cover to reinforcement in deck soffit = 60mm
d = 650 - 60 -32/2 = 574
As = Π162 × 1000 / 125 = 6434mm2/m
fy = 500N/mm2
fcu = 40N/mm2
z = [1 - ({1.1fyAs}/{fcubd})]d
z = [1 - ({1.1 × 500 × 6434}/{40 × 1000 × 574})]d = 0.85d < 0.95 d
∴ z = 0.85 × 574 = 488mm
MuSteel = 0.87fyAsz = 0.87 × 500 × 6434 × 488 × 10-6 = 1366 kNm/m
MuConcrete = 0.15fcubd2 = 0.15 × 40 × 1000 × 5742 × 10-6 = 1977 kNm/m > 1366
∴ Mu = 1366 kNm/m > 1137kNm/m ∴ OK.
Check Serviceability Limit State
Combination 1 SLS Design Moment = 842 kNm (345DL + 497LL)
Determine depth 'X' to neutral axis of cracked section:
cl. 4.3.2.1 Table 3
Youngs Modulus for concrete for short term loading = Ec = 31 kN/mm2
cl. 4.3.2.2
Youngs Modulus for steel reinforcement = Es = 200 kN/mm2
Case 1) When the bridge has just opened (when only a small amount of creep has occurred):
Modular Ratio = Es / Ec = 200 / 31 = 6.45
Taking first moments of area about the neutral axis:
1000 × X2 / 2 = 6.45 × 6434 × (574 - X)
500X2 + 41510X - 23.83×106 = 0
X = 177 mm
Second Moment of Area of cracked section:
Ixx = 1000×1773 / 3 + 6.45×6434×(574-177)2 = 8.39×109 mm4
Cl 4.1.1.3
Max compressive stress in concrete = 842×106 × 177 / 8.39×109 = 17.8 N/mm2
Table 2
Allowable compressive stress = 0.5fcu = 20 N/mm2 > 17.8 ∴ OK
Case 2) When creep and shrinkage in the bridge are substantially complete:
cl. 4.3.2.1(b)
Youngs Modulus for concrete for long term loading = Ec/2 = 15.5 kN/mm2
Hence Modified Ec for (345DL + 497LL) = (345 × 15.5 + 497 × 31) / 842 = 24.65 kN/mm2
cl. 4.3.2.2
Youngs Modulus for steel reinforcement = Es = 200 kN/mm2
Modular Ratio = Es / Ec = 200 / 24.65 = 8.1
Taking first moments of area about the neutral axis:
1000 × X2 / 2 = 8.1 × 6434 × (574 - X)
500X2 + 52115X - 30×106 = 0
X = 198 mm
Second Moment of Area of cracked section:
Ixx = 1000×1983 / 3 + 8.1×6434×(574-198)2 = 9.96×109 mm4
Cl 4.1.1.3
Max compressive stress in concrete = 842×106 × 198 / 9.96×109 = 16.7 N/mm2
Table 2
Allowable compressive stress = 0.5fcu = 20 N/mm2 > 16.7 ∴ OK
Tensile stress in reinforcement = 842×106 × (574 - 198) × 8.1 / 9.96×109 = 257.5 N/mm2
Table 2
Allowable tensile stress = 0.75fy = 375 N/mm2 > 257.5 ∴ OK
Crack Control:
Strain in reinforcement = ∈1 = 257.5 / 200000 = 0.00129
Table 13
Notional surface for crack calculation = 35mm cover to reinforcement
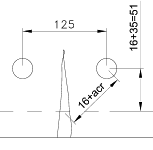
5.8.8.2
acr = √[(125/2)2 + (16+35)2] - 16 = 65
Allow for stiffening effect of concrete:
eqn 25
∈m = ∈1 - [{3.8bth(a'-dc)} / {∈sAs(h-dc)}] × [(1-Mq/Mg)×10-9]
∈m = ∈1 - [{3.8×1000×650×(625 - 198)} / {0.00129×6434×(650 - 198)}] × [(1 - 497/345)×10-9]
∈m = ∈1 - [-0.00012] but not greater than ∈1 Hence no stiffening effect
∈m = ∈1 = 0.00129 × (625 - 198) / (574 - 198) = 0.00146
Design crack width = 3 × 65 × 0.00146 / [1 + 2 × (65 - 35) / (650 - 198)] = 0.25 mm
eqn 24
Design crack width = 3acr∈m / [1+2(acr-cnom)/(h-dc)]
Table 1
Maximum allowable crack width = 0.25 mm ∴ OK
Combination 3 SLS Design Moment = 759 kNm (345DL + 414LL)
Determine depth 'X' to neutral axis of cracked section:
cl. 4.3.2.1 Table 3
Youngs Modulus for concrete for short term loading = Ec = 31 kN/mm2
cl. 4.3.2.1(b)
Youngs Modulus for concrete for long term loading = Ec/2 = 15.5 kN/mm2
Hence Modified Ec for (345DL + 414LL) = (345 × 15.5 + 414 × 31) / 759 = 23.95 kN/mm2
cl. 4.3.2.2
Youngs Modulus for steel reinforcement = Es = 200 kN/mm2
Modular Ratio = Es / Ec = 200 / 23.95 = 8.35
Taking first moments of area about the neutral axis:
1000 × X2 / 2 = 8.35 × 6434 × (574 - X)
500X2 + 53724X - 30.84×106
X = 200 mm
Second Moment of Area of cracked section:
Ixx = 1000×2003 / 3 + 8.35×6434×(574-200)2 = 10.18×109 mm4>
Cl 4.1.1.3
Max compressive bending stress in concrete = 759×106 × 200 / 10.18×109 = 14.9 N/mm2
Max compressive stress due to positive temperature difference = γfL × 2.31 = 0.8 × 2.31 = 1.8 N/mm2
Total compressive stress in concrete = 14.9 + 1.8 = 16.7 N/mm2
Table 2
Allowable compressive stress = 0.5fcu = 20 N/mm2 > 16.7 ∴ OK
Tensile stress in reinforcement = 759×106 × (574 - 200) × 8.35 / 10.18×109 = 232.8 N/mm2
Tensile stress due to reverse temperature difference =
γfL × 8.35×[{(1.43+0.06)×(130-60-16)/130}-0.06] = 0.8 × 4.7 = 3.8 N/mm2
Total tensile stress in reinforcement = 232.8 + 3.8 = 237 N/mm2
Table 2
Allowable tensile stress = 0.75fy = 375 N/mm2 > 237 ∴ OK
Hence B32 bars at 125 centres are adequate for the mid span.
Shear Design
Shear is designed for ultimate limit state.
cl. 5.4.4
V = shear force due to ultimate loads.
Maximum Dead Load V = γf3 × 12 × (1.15 × 16.3 + 1.75 × 2.4) / 2
Maximum Dead Load V = 1.1 × 137.7 kN = 151 kN
Determine shear effects at distance d away from the support.
Try 32mm dia. bars at 125 c/c : d = 574mm
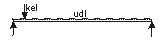
Maximum HA V = γf3 × 1.5 × (12 × 17.5 / 2 + 33 × 11.426 / 12 - 17.5 × 0.574)
Maximum HA V = 1.1 × 190 kN = 209 kN
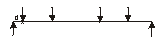
Maximum HB V = γf3 × 1.3 × 75 × (11.426 + 9.626 + 3.626 + 1.826) / 12
Maximum HB V = 1.1 × 215 kN = 237 kN > 209 ∴ HB loading critical
Maximum V = 151 + 237 = 388 kN
Shear stress = V / bd = 388×103 / (1000 × 574) = 0.68 N/mm2
Design for no shear reinforcement condition then ξsvc > 0.68 N/mm2
Table 9
ξs = (500/d)1/4 = (500/574)1/4 = 0.97
Table 8
vc = 0.27/γm(100As/bwd)1/3(fcu)1/3
vc = (0.27 / 1.25) × [100 × 6434 / (1000 × 574)]1/3 × (40)1/3 = 0.77 N/mm2
ξsv√ = 0.97 × 0.77 = 0.75 N/mm2 > 0.68 ∴ OK
cl 5.3.3.1
Check that the maximum allowable shear stress is not exceeded:
Maximum allowable shear stress = 0.75√fcu or 4.75 N/mm2
0.75√fcu = 0.75√40 = 4.74 > 0.68 ∴ OK
Hence B32 bars at 125 centres are adequate for shear at the ends of the deck.
Note: Intermediate sections between mid span and the ends of the deck will have a smaller moment than at mid span and a small shear than at the ends of the deck. These sections need to be checked to determine where the reinforcement may be reduced to B25 at 125c/c.
cl. 5.8.4.1
Minimum area of reinforcement = 0.15% of bad = 0.15 × 1000 × 574 / 100 = 861 mm2/m ∴ use B12 bars at 125 centres (As = 905 mm2/m) for distribution reinforcement.
Contact David Childs