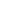Design a simply supported beam which carries a 150mm thick concrete slab together with a nominal live load of 10.0 kN/m² . The span of the beam is 9.0m centre to centre of bearings and the beams are spaced at 3.0m intervals. The slab will be assumed to be laid on top of the beams with no positive connection to the compression flange.

γ_conc. = 24kN/mm³

Loading per beam (at 3.0m c/c)

Nominal Dead Loads :

slab = 24 × 0.15 × 3.0 = 10.8 kN/m

beam = say 2.0 kN/m

Nominal Live Load : = 10 × 3.0 = 30 kN/m
 

Load factors for ultimate limit state from BS 5400 Part 2 Table 1:

Dead Load:

γ_fL steel = 1.05

γ_fL concrete = 1.15

Live Load:

γ_fL HA = 1.50
 

Total load for ultimate limit state:

= (1.15 × 10.8)+(1.05 × 2.0)+ (1.5 × 30) = 60 kN/m

Design ultimate moment = 60 × 9.0² / 8 = 608 kNm

Design ultimate shear = 60 × 9.0 / 2 = 270 kN
 

1) Design for Bending

Use BS EN 10 025 steel grade S275, then nominal yield stress σ_y = 265 N/mm²

Approximate modulus required:

= M × γ_m × γ_f3 / σ_y

= 608 × 1.2 × 1.1 × 10⁶ / 265 =  3.03 × 10⁶ mm³
 

Try a 610 × 229 × 125kg/m UB (Z_× = 3.222 × 10⁶, Z_p = 3.677 × 10⁶)

Check for compact section:

web:

web depth = 547; and m = 0.5

34t_w(355/σ_yw)^0.5/m = 34 × 11.9 × (355/265)^0.5/0.5 = 937

547 < 937 ∴ web OK

compression flange:

b_fo = (229 - 11.9 - 2*12.7)/2 = 96

7t_fo(355/σ_yf)^0.5 = 7 × 19.6 × (355/265)^0.5 = 159

96 < 159 ∴ flange OK

Hence section is compact.
 

Determine Effective Length:

l_e = k₁ k₂ k_e
k₁ L = 1.0 (flange is free to rotate in plan)
k₂ = 1.0 (load is not free to move laterally)
k_e = 1.0 (check later for initial value)
L= 9000mm
l_e = 1.0 × 1.0 × 1.0 × 9000 = 9000mm
 

Slenderness:

Half wavelength of buckling = l_w = L = 9000mm
M_pe = Z_pe × σ_yc
M_pe = 3.677 × 10⁶ × 265 × 10^-6 = 974kNm

λ_LT = l_e k₄ ην / r_y
k₄ = 0.9
η = 0.94 (From Fig. 9(b): M_A/M_M = M_B/M_A = 0)
λ_F = l_e/r_y(t_f/D)
λ_F = 9000/49.6 (19.6/611.9) = 5.81
i = I_c/(I_c+I_t)
i = 0.5
ν = 0.78 (from Table 9)
λ_LT = 9000 × 0.9 × 0.94 × 0.78 / 49.6 = 120

Limiting moment of resistance: λ_LT ((σ_yc/355)(M_ult/M_pe))^0.5
Section is compact, hence M_ult = M_pe = 974kNm
λ_LT ((σ_yc/355)(M_ult/M_pe))^0.5  = 120 × ((265/355)(974/974))^0.5 = 104
l_e/ l_w = 1.0
From Fig.11_(b) : M_R/M_ult  = 0.42
M_R = 0.42 × M_ult = 0.42 × 974 = 409 kN/m

M_D = M_R /γ_m γ_f3
M_D = 409 / (1.2 × 1.1) = 310 kNm < 608 kNm
hence section too small.

{Note: If the compression flange is cast into the deck slab then l_e = 0 (cl.9.6.4.2.1) which results in
M_R = M_ult =  974 kNm giving  M_D = 974 / (1.2 × 1.1) = 738 kNm > 608 kNm}

Approx. Zpe required = 608/310 × 3.677×10⁶ = 7.21 × 10⁶ mm⁴
Use a 762 × 267 × 197kg/m UB
Z_pe = 7.167 × 10⁶ mm³
M_pe = 7.167 × 10⁶ × 265 × 10^-6
M_pe = M_ult = 1899kNm

Section is compact
λ_F = 5.2
ν= 0.81
λ_LT = 108
M_R/M_ult = 0.51
M_D = 733 kNm > 608 hence OK

Check effect of assuming ke = 1 (cl.9.6.4.2.1)

M_D / M_ult = 733 / 1899 = 0.39
From fig. 11(b) : λ_LT((σ_yc/355)(M_ult/M_pe))^0.5 = 110
giving λ_LT = 127
λ_LT = l_e k₄ ην / r_y
approx le = (110×57.1) / (0.9×0.94×0.81) = 9166
Hence k_e maximum = 9166 / 9000 = 1.018

k_e² = 1/[1-(60Et_fβδ_tR_v/(W[L/r_y]³ν⁴ ))]
R_v/W = 0.5 (load causing max moment in beam)
E = 205 000  (cl.6.6)
t_f = 25.4
β = 1.0
ν = 0.81
L/r_y = 9000 / 57.1
Hence max δ_t = 0.000378 mm

Effective section for bearing stiffener :

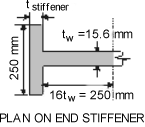
The ends of bearing stiffeners should be closely fitted or adequately connected to both flanges (cl.9.14.1). Hence the compressive edge of the bearing stiffener is fully restrained at the point of maximum bending. Therefore yield stress can be developed in both tension and compression edges of the bearing stiffener (λ_LT = 0).

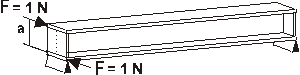
Deflection of cantilever :
δ_t = F a³ / 3 E I
0.000378 = 1×(744.2)³ / (3×20500× I )
I = 1.773 × 10⁶ mm⁴
I of end stiffener :
I = 250×15.6³/12 + t×250³/12
t min = 1.3 mm
Use at least 10mm plate hence OK

Try 10mm end plate and check bearing stiffener :
I = 250×15.6³/12 + 10×250³/12 = 13.1×10⁶ mm⁴ 
δ_t = 1×(744.2)³ / (3×205000×13.1×10⁶) = 51×10^-6 mm/N

End stiffeners have to be provided to support the compression flange for a pinned end condition (k₁ = 1.0 in cl.9.6.2).

F_s1 = 0.005(M/(d_f{1-(σ_fc/σ_ci)²}))
d_f = 769.6 - 25.4 = 744mm
σ_fc = M / Zxc = 608×10⁶ / 6.234×10⁶ = 97.5 N/mm²
σ_ci = π²ES/λ_LT²
S = Z_pe/Z_xc = 7.167 / 6.234 = 1.15
σ_ci = π² × 205000 × 1.15 / 108² = 199 N/mm²
F_s1 = 0.005(608×10⁶/(744{1-(97.5/199)²}))×10^-3
F_s1 = 5.4 kN

F_s2 = β (Δ_e1 + Δ_e2)σ_fc / ((σ_ci - σ_fc)Σδ)
Δ_e1 = Δ_e2 = D/200 = 769.6 / 200 = 3.848
β = 1
Σδ = 2δ_t = 2 × 51×10^-6 = 0.102 × 10^-3
σ_ci is to be determined using l_e from 9.6.4.1.1.2b).
l_e = πk₂(EI_c(δ_e1+δ_e2)/L)^0.5
I_c = 25.4 × 268³ / 12 = 40.7 × 10⁶
l_e = π × 1.0(205000 × 40.7 × 10⁶ × 2 × 51 × 10^-6 / 9000)^0.5 = 967mm
λ_F = (l_e/r_y)(t_f/D) = (967/57.1)(25.4/769.6) = 0.559
ν = 0.993 (From Table 9)
λ_LT = l_ek₄ην/r_y = 967 × 0.9 × 1.0 × 0.993 / 57.1 = 15.1
σ_ci = π²ES/λ_LT²
σ_ci = π² × 205000 × 1.15 / 15.1² = 10205 N/mm²
F_s2 = 3.848 × 97.5 / ((10205 - 97.5) × 0.102 × 10^-3) × 10^-3
F_s2 = 0.4 kN

Assume no camber is provided to the beams and the bearings are aligned square to the longitudinal axis of the beam, then :
F_s3 = Rd_L(Δ/D+θ_Ltanα)/D
α = 0
R = 60 × 9 / 2 = 270 kN
d_L = 810 say (allow 40mm for depth of bearing)
F_s3 = 270 × 0.81 × ( 1/200 ) / 0.77 = 1.4 kN

Bearings are aligned square to the longitudinal axis of the beam :
Hence F_s4 = 0

F_s = 5.4 + 0.4 + 1.4 + 0 = 7.2 kN
Allowing additional effect for wind load ( which is generally small compared to F_s ) then
say F_s = 9 kN

Moment at base of stiffener = 9 × ( D - 1.5 × t_f )

M = 9 × ( 769.6 - 1.5 × 25.4 ) × 10^-3 = 6.6 kNm

Bending capacity of stiffener = Z_xc × σ_yc / (γ_m × γ_f3)

M_D = 6.6 × 10⁶ = Z_xc× 265 / ( 1.2 × 1.1 )

Z_xc = 32.9 × 10³ mm³

Portion of web plate = 16t_w= 16 × 15.6 = 250mm

Z_xc = t_stiffener × 250²/6 + 250 × 15.6²/6

Hence t_stiffener = 2.2mm < 10mm therefore 10mm plate is satisfactory.

Use 762 × 267 × 197 kg/m UB with 10mm thick end bearing stiffener.