
List of Reinforced Concrete Design Standards: [Show]
• EN 1991-1-1: Actions on Structures - General Actions
• EN 1991-1-4: Actions on Structures - Wind Actions
• EN 1991-1-5: Actions on Structures - Thermal Actions
• EN 1991-1-7: Actions on Structures - Accidental Actions
• EN 1991-2: Actions on Structures - Traffic Loads on Bridges
• EN 1992-1-1: Design of Concrete Structures - General Rules
• EN 1992-2: Design of Concrete Structures - Bridges
• Each document is accompanied by a National Annex
British Standards
• BS 4449: Steel for Reinforcement of Concrete
• BS 5400: Part 2: Specification for Loads
• BS 5400: Part 4: Code of Practice for the Design of Concrete Bridges
• BS 8500: Concrete - Complementary British Standard to BS EN 206-1
• BS 8666: Specification for scheduling, dimensioning, bending and
cutting of steel reinforcement for concrete
Design Manual for Roads and Bridges
• BA24: Early Thermal Cracking of Concrete
• BD24: Design of Concrete Bridges
• BD28: Early Thermal Cracking of Concrete
• BD37: Loads for Highway Bridges
• BD43: Criteria and Materials for the Impregnation of Concrete
Highway Structures
• BD57 and BA57: Design for Durability
Technical Papers
• CIRIA Report C660 - Early-age thermal crack control in concrete.
Reinforced Concrete Decks
The three most common types of reinforced concrete bridge decks are :

Solid Slab

Voided Slab

Beam and Slab
Solid slab bridge
decks are most useful for small, single or multi-span bridges and are
easily adaptable for high skew.
Voided slab and beam and slab bridges are used for larger, single or multi-span
bridges. In circular voided decks the ratio of [depth of void] / [depth
of slab] should be less than 0.79; and the maximum area of void should
be less than 49% of the deck sectional area.
Analysis of Deck
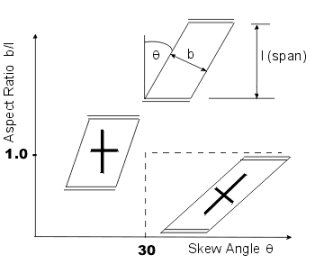
For decks with skew less than 25° a simple unit
strip method of analysis is generally satisfactory. For skews greater
than 25° then a grillage or finite element method of analysis will
be required. Skew decks develop twisting moments in the slab which become
more significant with higher skew angles. Computer analysis will produce
values for Mx, My and Mxy where Mxy represents the twisting moment in
the slab. Due to the influence of this twisting moment, the most economical
way of reinforcing the slab would be to place the reinforcing steel
in the direction of the principal moments. However these directions
vary over the slab and two directions have to be chosen in which the
reinforcing bars should lie. Wood and Armer have developed equations
for the moment of resistance to be provided in two predetermined directions
in order to resist the applied moments Mx, My and Mxy.
Extensive tests on various steel arrangements have shown the best positions
as follows
Bridge Components | Choice of Deck
