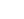Grillage Analysis of Bridge Decks
Index
Grillages are most widely used to analyse beam and slab type bridge decks. Solid slab type decks are generally modelled using finite elements, however grillages may be used for this type of deck with reasonably accurate results.
Longitudinal grillage members are arranged to represent the main beams with transverse members representing the deck slab and diaphragm beams.
The spacing of transverse grillage members are chosen to be about 1.5 times the spacing of the main longitudinal members, but may vary up to a limit of 2:1. Transverse members are required at the diaphragm positions and, in order to achieve a member at mid span, there needs to be an odd number of members.
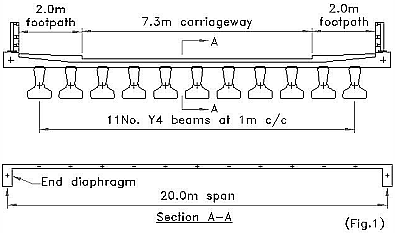
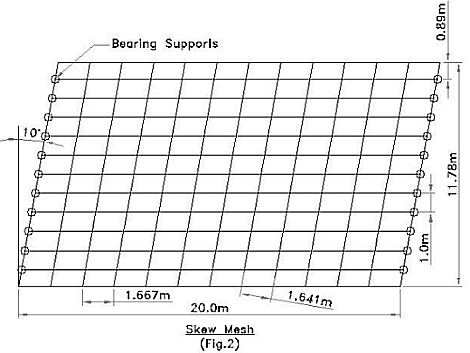
In the case of skew decks the transverse members should be arranged orthoganally to the main members (see Fig.3) to achieve the correct magnitude for moments and deflections. However this arrangement can be impractical for small skew angles (below 35o) and a skew mesh is usually adopted (see Fig.2). The skew mesh will tend to slightly overestimate the magnitude of moments and deflections and is therefore considered to be a safe solution. The section properties of transverse members in skew meshes should be calculated using the orthoginal spacing; the width of the transverse member in Fig.2 being 1.641m and not 1.667m.
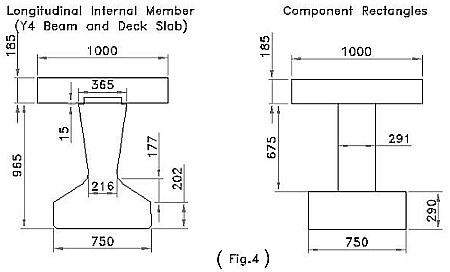
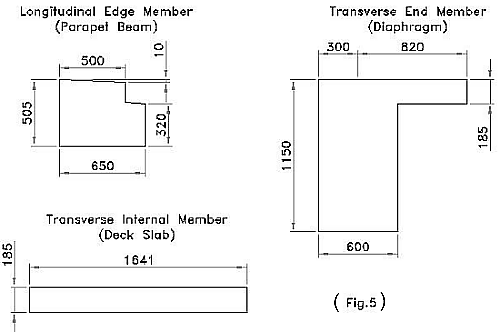
The bending inertia and torsional inertia are required for all the members in the grillage model. The sections for the members representing the deck in Fig.1 are shown in Fig.4 and Fig.5 below.
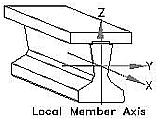
The bending interia for the composite sections can be calculated using a suitable proforma. An Excel spread sheet using co-ordinate geometry can be downloaded by clicking here. Member properties for the grillage are calculated for the local member axis as shown and care will be needed to ensure you are using the correct notation. If the spread sheet is used then Ixx from the spread sheet will be input as Iy for the local member axis shown. Similarly Iyy from the spread sheet will be input as Iz and the torsional inertia J will be input as Ix.
An approximation of the torsional inertia of the member is obtained by dividing the section into component rectangles as shown in Fig.4.
The torsional inertia for a rectangle is given by J=k1b3bmax
where:
b is the length of the short side
bmax is the length of the long side
k1={1-0.63(b/bmax)(1-b4/12b4max)}/3
The torsional inertia of the section is the summation of the inertias of the individual rectangles. As the deck slab is used in both the longitudinal members and transverse members then the inertia of this rectangle is halved. This only relates to the Torsional Inertia, the full section is used to calculate the Bending Inertia.
The calculator below can be used to check that the Torsional Inertia of the Longitudinal Internal Member in Fig.4 is:
J=(0.5 * 1864 + 4042 + 4613)*106 = 9587*106mm4
Similarly the Torsional Inertia of the Transverse Internal Member (Deck Slab 1641x185) in Fig.5 is:
J=(0.5 * 3216)*106 = 1608*106mm4
When the deck is cantilevered from the edge of the main deck beams it is convenient to extend the grillage to the parapet beam as shown in Fig.1, 2 and 3. This will simplify the application of footway loading and accidental wheel loading.
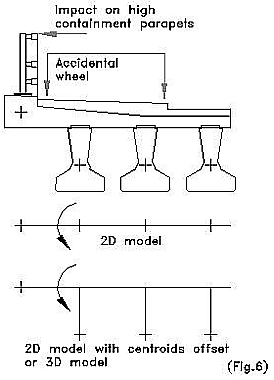
However the torsional effects in the edge beam can be significantly overestimated in a beam and slab type deck if the members are not modelled correctly.
Most of the cantilever effects should induce bending in the deck slab with secondary torsional effects being induced in the supporting edge beams.
If a simple two dimensional (2D) grillage is used then the bending effects from the cantilever will be resisted by torsion in the edge beam. This will overestimate the torsion in the edge beam and underestimate the bending in the deck.
Some grillage programs allow the centriods of the members to be offset from the 2D plane (as shown in Fig.6). Alternatively a three dimensional model may be used by including rigid, vertical, dummy members into the model, although this solution does make the geometry more complicated.
Most grillage programs will allow the supports to be modelled as free, rigid or sprung. Spring supports are used to model the elastic deformation either of the bearing or of the support structure. Rubber bearings will distort under load and have a significant effect on the distribution of loads throughout the deck. Even the elastic deformation of concrete columns can have an effect on the distribution of loads in a continuous deck.
A simple line beam analysis will give an approximate magnitude for the reactions. This will enable a suitable bearing to be chosen for the grillage model. Alternatively the grillage analysis can be carried out with rigid vertical supports and modified later.
Using the bearing layout shown at the bottom of the Choice of Bearings web page:
- 'Free and sliding-guided bearings' will be fixed or sprung in the vertical direction and releases applied for rotational directions.
- The 'Fixed' bearing will be fixed or sprung in all directions.
When using spring supports it is usual to have to fix one bearing in the vertical direction to achieve a stable solution.
A grillage does not analyse in-plane loading so any longitudinal or transverse restraint will not be modelled.
All loading is proportioned to the grillage members and grillage joints (nodes) before the moments, shears and torsions are calculated. Many programs have the facility for applying patch loads and point loads which do not necessarily coincide with joints or members. The program will distribute these loads to the members before calculating the moments, shears and torsion effects.
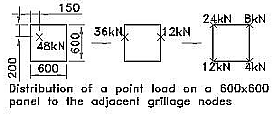
There are a number of ways of proportioning the loads to the joints if the program does not have this facility. The 48kN point load shown acting within a 600 square grid can be proportioned to a pair of opposite members and then again to the joints as shown. This distribution will achieve sufficiently accurate results.
It is convenient to apply all loads to the structure as nominal loads. Load factors can be applied to the combination cases to avoid inputting numerous load cases. Consequently load cases should not be too complex. For example carriageway construction 150mm thick is considered in BD21 as 100mm surfacing with 50mm fill and should be applied as two load cases as different load factors are applied to fill than to surfacing.
Dead load is applied to the main longitudinal members. Some programs will automatically generate dead load by applying a density to the cross-sectional area of the member. Care is needed to avoid double accounting for the weight of the deck slab.
Superimposed dead load (carriageway surfacing, footpath fill and surfacing and parapets) are input as uniformly distributed loads along the length of the longitudinal grillage members. Some programs have the facility of applying patch loads which can be used for the surfacing providing it is of constant thickness.
Live loading can consist of HA (udl + kel) load, HB load, Pedestrian load, Accidental Wheel load and Wind load. Collision load on parapets is only included if high containment parapets are required. Horizontal loads such as traction or braking and skidding are generally not included as the deck is very stiff for resisting horizontal loads compared with vertical loads. Unless the deck has a very high superelevation or steep longitudinal gradient then the load component in the vertical direction for skidding and centrifugal loads will be negligible.
It is always good practice to carry out approximate checks of the output as the job proceeds. One simple check is to obtain the total reactions for each load case to see if they agree with an estimate of the total load applied in each load case.
Also a simple line beam beam analysis will produce approximate moments and shears that can be compared with the results from the grillage.
An Excel spread sheet using moment distribution to carry out a line beam analysis can be downloaded by clicking here.
Contact David Childs