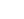Reinforced Concrete to BS 5400 Part 4
Index
1. Introduction
Both the Serviceability and Ultimate Limit States need to be considered.
Serviceability Limit State ensures that crack widths do not exceed values specified for different environmental conditions, and also ensures that concrete and reinforcement stresses are maintained below a safe limit.
Ultimate Limit State ensures that the structure will not collapse.
2. Serviceability Limit State
i) Crack Control
Cracks in concrete can be caused by:
- corrosion of the reinforcement which causes the concrete to spall
- thermal movements, particularly cooling from heat of hydration (called early thermal cracking)
- structural actions such as bending, shear or torsion
Corrosion of reinforcement is controlled by use of suitable concrete grades and providing adequate cover to the reinforcement.
Cracks due to thermal movements are controlled by providing minimum nominal steel area and restricting the maximum bar spacing. BD28/87 is used to calculate the minimum steel area and bar spacing to control early thermal cracking.
The width of shear cracks is controlled by ultimate strength calculations.
Only the crack widths caused by bending and tension need to be calculated and clause 5.8.8.2 is used.
For calculating the crack width only combination 1 loading is used and a maximum of 30 units of HB is applied. Cracks caused by higher loadings will not exist for long enough to affect corrosion. The maximum design stress limits will ensure that the cracks close up when the loads are removed.
A cracked elastic section analysis is used to determine the strain εm at the level where cracking is being considered.
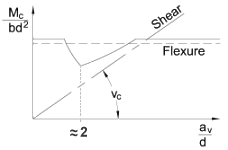
Using a rectangular section as an example:
We first need to determine the position of the neutral axis. Let:
αe = Es / Ec
Es = 200kN/mm2 (clause 4.3.2.2)
The short term value of Ec is obtained from Table 3 which is appropriate to the live load portion of the moment (Mq). The permanent load portion of the moment (Mg) has an Ec value equal to half the short term value. The modified value of Ec used for the crack width calculation is an intermediate value between the short and long term values (clause 4.3.2.1(b)).
Modified Ec = Ec(short-term){1-0.5[Mg/(Mg+Mq)]}
ρ = As / btd and ρ' = A's / btd
Then dc/d = √{[αeρ + (αe - 1)ρ']2 + 2[αeρ + (αe - 1)ρ'd'/d]} - [αeρ + (αe - 1)ρ']
Second Moment of Area of Cracked Section Ic = btdc3/3 + (αe-1)As'(dc-d')2 + αeAs(d-dc)2
Strain at level of tension reinforcement εs = αe(Mg+Mq)(d-dc) / (IcEs)
Depth to notional surface where nominal cover cnom is provided = a'
Strain at notional surface ε1 = εs(a'-dc) / (d-dc)
There is a correction formula (equation 25 in clause 5.8.8.2) which allows for the stiffening effect of concrete in the tension zone. Due to fatigue the stiffening effect does not work under fluctuating load. This is allowed for in equation 25 by providing no advantage if more than half the moment is due to live load.
The corrected strain at notional surface εm is thus obtained using the value of ε1 in equation 25.
acr = √{(cnom+Φ/2)2 + (s/2)2} - Φ/2
The Design Crack Width can now be calculated using equation 24 in clause 5.8.8.2.
ii) Stress Limits
The methods given in the code for checking crack widths assumes a linear elastic behaviour. It is therefore necessary to check the stress limits to ensure this assumption is correct. in particular that the strains caused by transient loads will not become permanent.
The stresses are calculated using a cracked elastic section analysis similar to that used to determine the crack width described above. All load combinations need to be checked to ensure that the stress limits are not exceeded.
The stress limits are given in Table 2 of the code which are:
0.75fy for reinforcement in tension or compression. This is critical for most members in bending.
0.5fcu for concrete in compression with triangular stress distribution. This is critical for members in bending with significant axial load or with heavy reinforcement.
0.38fcu for concrete in compression with uniform stress. this is critical for members in axial compression.
3. Ultimate Limit State
To determine the moment of resistance of a member at failure by limit state analysis the following assumptions are made:
- The distribution of strain across any section is linear. This means that plane sections before bending remain plane after bending, and the strain at any point is proportional to its distance from the neutral axis.
- The resistance of concrete in tension is ignored.
- The relationship between the stress and strain in the reinforcement is as shown in Figure 2 of the code with γm = 1.15.
- The relationship between the stress and strain in the concrete is as shown in Figure 1 of the code with γm = 1.5. The strain in the concrete at the outermost fibre is taken as 0.0035. Alternatively the distribution of stress in the concrete at failure may be represented by a uniform stress of 0.4fcu acting over the whole of the compression zone.
The deisgn formulae given in clause 5.3.2.3 of the code are based on a uniform compressive stress of 0.4fcu for concrete and stresses of 0.87fy in tension and 0.72fy in compression for steel. The steel stresses are the maximum values provided by the stress-strain curves, where 0.72fy is a simplification of the expression for steel in compresssion.
The design formulae are also based on a maximum depth of concrete in compression of 0.5d; this ensures a strain ≥ 0.0035 in the tension reinforcement. For values of x > 0.5d the use of the design stress of 0.87fy in tension is invalid, the design becomes inefficient and the failure less ductile.
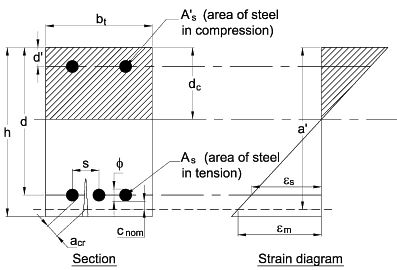
For the singly reinforced rectangular section:
Taking moments about the centre of compression for the tensile force
Mu = (0.87fy)Asz
Taking moments about the centre of tension for the compressive force
M = (0.4fcu)bxz = (0.4fcu)bx(d - 0.5x)
The maximum moment of resistance is obtained when x = 0.5d so substituting for x we get:
Mu = 0.15fcubd2
The depth to the neutral axis depends upon the reinforcement provided and is obtained by equating the forces:
(0.87fy)As = (0.4fcu)bx
Rearranging and dividing both sides by d we get:
(x/d) = (2.2fyAs) / (fcubd)
Lever arm z = (d - 0.5x) so substuting for x we get:
z = (1 - [1.1fyAs] / [fcubd])d
The value of z is not to be taken greater than 0.95d.
For the doubly reinforced rectangular section:
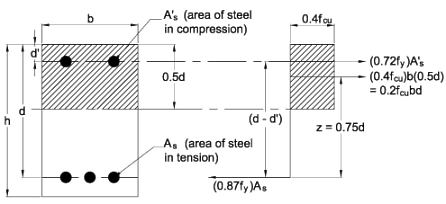
Taking moments about the centre of tension for the compressive forces
Mu = 0.15fcubd2 + (0.72fy)A's(d - d')
Equating the tensile and compressive forces
(0.87fy)As = 0.2fcubd + (0.72fy)A's
These two equations are based on a value of d'/d ≤ 0.2, which ensures a strain ≥ 0.0035 x 0.6 = 0.0021 in the compression reinforcement. For values of d'/d > 0.2 the use of a design stress of 0.72fy in compression becomes invalid.
4. Shear
The design rules for shear in beams are based on the results of tests carried out on beams with and without shear reinforcement.
The results from the beams tested without shear reinforcement showed that for a constant concrete strength and longitudinal steel percentage, the relationship between the ratio of the bending moment at collapse (Mc) to the calculated ultimate flexural moment (Mu) and the ratio of shear span (av) to effective depth (d) is as shown below:
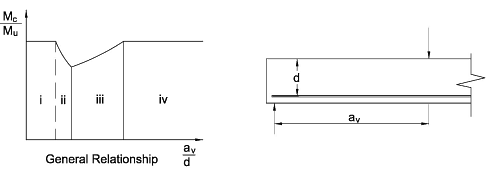
The diagram has four distinct regions, each of which has a different mode of failure.
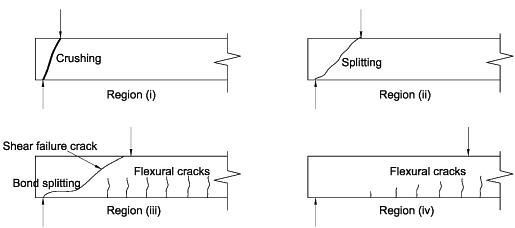
Region (i) fails by crushing of a compression strut running from the load to the support.
Region (ii) fails by diagonal tension causing splitting along the line from the load to the support.
Region (iii) fails when a flexural crack develops into a shear crack.
Region (iv) fails in flexure.
The flexural failure in region (iv) is prevented by designing the beam for Mu in accordance with Clause 5.3.2.3. The test results show that this is unsafe for regions (ii) and (iii) and Mc needs to be controlled by considering the shear force.
Let the shear force at failure = Vc and the nominal shear stress vc = Vc / bd then:
Mc = Vcav = vcbdav
The test results relationship with av/d can be reproduced by dividing both sides of the above equation by bd2 which gives:
Mc/bd2 = vc av/d
The dashed line is Mu/bd2 which assumes flexural failure. The chain dotted line is constructed to cut off the unsafe side of the graph; the slope of this line is vc and is the allowable shear stress.
Values of vc are given in Table 8 of the code; these values will ensure that the moment to cause collapse will fall below the test values. It can be seen from Table 8 that the steel area As has a more significant effect on the value of vc than does the concrete strength.
When the shear stress v is greater than ξsvc, as given in Table 7 of the code, then links need to be designed. These are designed on the basis that the beam and links act as a pin-jointed truss.
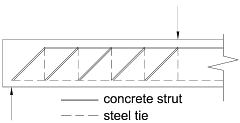
The links are designed to carry the shear in excess of that which can be carried by the concrete. The horizontal tie force in the truss analogy has to be provided by the tension reinforcement, this is in addition to that required to resist any bending effects and is determined from Asa ≥ V/{2(0.87fy)} in clause 5.3.3.2.
The beam may fail by crushing of the compression struts regardless of the amount of shear reinforcement. The maximum allowable shear stress is therefore limited to a value of 0.92√(fcu/1.5) as given in clause 5.3.3.1.
Contact David Childs