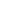Eurocode Traffic Loading Idealisation for Grillage Analysis of Bridge Decks
Index
LM1 (TS + UDL) | LM3 (SV100) | Footway Loading | Accidental Vehicle Load on Footway | Collision Forces on Vehicle Restraint System
Using a prestressed Y4 beam with reinforced concrete deck slab as the deck example as shown in Fig.1; the deck having a 10° skew, a span of 20m and carrying a 7.3m carriageway with two 2m footpaths.
EN 1991-2:2003 Cl.4.2.3
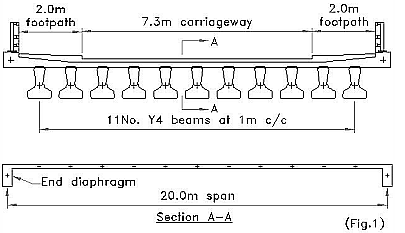
7.3m carriageway has 2No. 3m notional lanes with remaining area width of 1.3m UK NA Cl.2.16 The deck shall carry STGO vehicle SV100 UK NA Cl.2.30.1 Assume bridge requires high containment metal parapets : Class C collision loading needs to be considered.
LM1 (TS +UDL)
The UDL can be applied to each longitudinal member as a uniformly distributed load, the intensity of the load is proportional to the width of the lane directly above the longitudinal member, for example:
EN 1991-2:2003 Cl 4.3.2(1)(b) UDL = αqqk kN/m2 of notional lane.
EN 1991-2:2003 Table 4.2 qk (kN/m2) = 9 (lane 1) & 2,5 (all other lanes and remaining area).
UK NA to BS EN 1991-2:2003 Table NA.1 αq = 0,61 (lane 1) & 2,2 (all other lanes and remaining area).
UDL/m width = 9 x 0,61 = 5,5 kN/m (lane 1)
& 2,5 x 2,2 = 5,5 kN/m (all other lanes and remaining area).
UDL on member 2 = 0.15 x 5,5 = 0,83kN/m
UDL on members 3 & 4 = 1,0 x 5,5 = 5,5kN/m
UDL on member 5 = 0,85 x 5,5 = 4,68kN/m
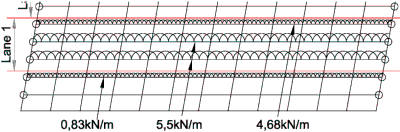
UDL applied to each longitudinal grillage member to represent UDL in lane 1.
Alternatively, if the program has the facility of applying patch loads then a patch width equal to the lane width and length equal to the loaded length may be applied. The patch load is usually positioned by the centroid of the patch area in relation to the grid co-ordinates.
A line beam analysis is useful for determining the critical positions of the TS system before carrying out the grillage analysis. This can reduce the number of load cases required; particularly if the deck has several continuous spans. The tandem system (TS) can be applied as point loads to the grillage to represent the wheel loads. As loads are initially proportioned to the adjacent members and joints then the worst effects will always be achieved by positioning one of the axles directly above a transverse member. If the deck is skewed then the postion of the TS to give the worst effect will be different to a square deck and two or three positions may need to be checked to find the critical case.
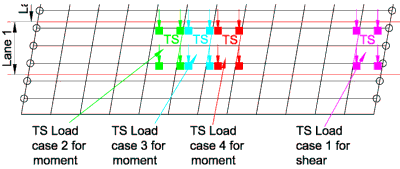
It is therefore useful to separate the UDL and TS systems into different load cases to avoid repeating the calculation for the effects of the UDL. The UDL and the various positions of the TS can be added together in different combination cases in the grillage program.
Similar load cases are produced for the UDL and TS systems in the second lane.
Group gr5 also contains the UDL and TS loadings in combination with the SV or SOV vehicles. All these variations in load cases can be developed in the combination cases in the grillage program.
The SV100 vehicle consists of six axles with two wheels on each axle and is applied to the grillage as a series of point loads.
Each axle load is multiplied by a Dynamic Amplification Factor of 1.12 and the load shared equally between the wheels. Figure NA.1 of the UK NA to BS EN 1991-2:2003 allows the wheel loads to be applied as patch loads however there is little to be gained in a global analysis by applying this refinement and point loads will be a suitable representation for the wheel loads.
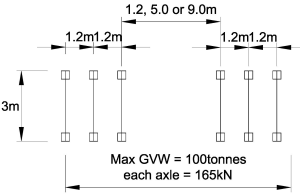
Each axle is to be multiplied by the Dynamic Amplification Factor (DAF = 1.12 for a basic axle load of 165kN)
There are three variations of the inner axle spacing for the SV vehicle that can be applied to the deck. A line beam analysis incorporating moving point loads will indicate the positions of the critical SV vehicle to achieve the design moments and shears.
An Excel spread sheet using moment distribution to carry out a line beam analysis of standard moving vehicles can be purchased by clicking here.
The
result
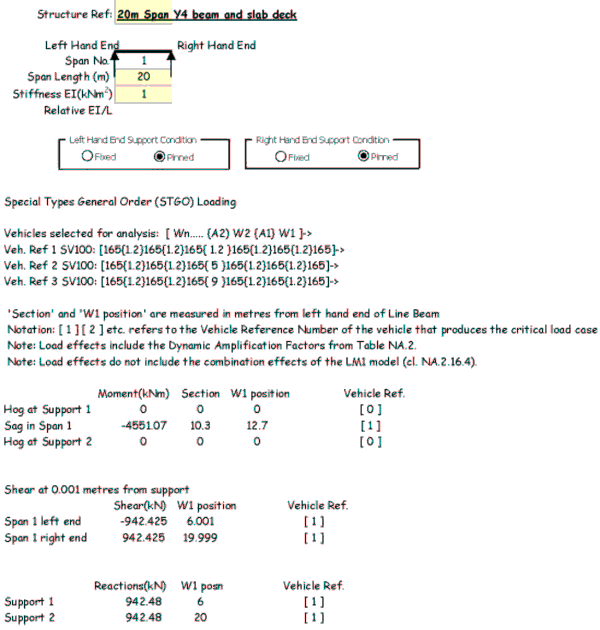of the line beam analysis shows that the maximum sagging moment occurs at 10.3m from the end of the deck with the leading axle at 12.7m from the end.
The result of a line beam analysis shows that the maximum sagging moment occurs at 10.3m from the end of the deck with the leading axle at 12.7m from the end.
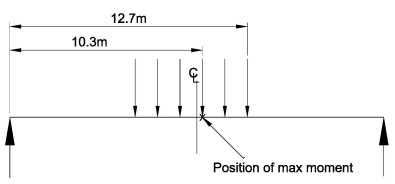
As the loading is symmetrical and both ends of the single span deck are simply supported then the position of maximum moment can be measured from either end of the deck.
The transverse position of the SV vehicle for the worst effect will depend on which member is being considered, however it is usual to design all internal beams for the critical loading condition for vehicles on the carriageway. The SV vehicle can encroach up to 500mm into the adjacent lane before any reduction is made to the associated Load Model 1 loading in the adjacent lane. The edge beams will require special consideration to support the additional loading from the cantilever.
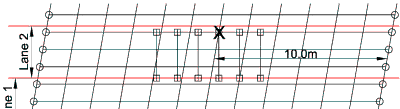
The diagram shows one of the wheels on the critical axle positioned over the nearest transverse member at 10.0m from the support.
This would produce the critical loading condition for the bending moment on the internal beam for an orthoganal deck, however other positions need to be considered to take account of the skew effects.
As a check on the data, the total of the reactions should equal the total load of the vehicle = 6 x 165 x 1.12 = 1108.8kN. Also the line beam analysis gives a total sagging moment of 4551kNm; so as there are approximately four longitudinal members supporting the vehicle, then the moment from the grillage should be in the order of 4551 / 4 ≅ 1140kNm in the longitudinal member.
EN 1991-2:2003 Clause 5.3.2.1(1) states that the pedestrian live load shall be taken as 5.0 kN/m2, but reduced to 0.6 x 5.0 = 3.0kN/m2 when used in combination with load system LM1 for load group gr1a. The UDL can be applied to members below the footways in a similar manner to the UDL described in Section 1. above. However, as there is no barrier between the carriageway and footway, Clause 4.7.3.1(2) requires that the footway members are designed for one Accidental Axle Load (200kN) which is generally more onerous than the pedestrian live load.
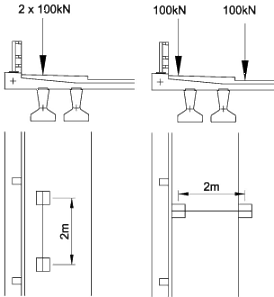
Accidental Axle Loading consists of a two wheeled, 200kN axle and is applied to the grillage as two point loads. The wheel loads may be applied as patch loads (400mm x 400mm) however there is little to be gained in a global analysis by applying this refinement and point loads will be a suitable representation for the wheel loads.
Similarly as with the TS system and SV vehicle a line beam analysis incorporating moving point loads will indicate the critical positions of the accidental axle load to achieve the worst moments and shears.
An Excel spread sheet using moment distribution to carry out a line beam analysis of standard moving vehicles can be downloaded by clicking here. The Abnormal Load facility may be used in the line beam proforma to input the accidental axle load.
There are two orientations shown for the accidental axle load, however as the beams are closely spaced then the condition with both wheels sitting on one beam will produce the worst load effects for that beam and the second option need not be considered for this example.
The
result
of the line beam analysis shows that the maximum sagging moment occurs at 10.5m from the end of the deck under the leading wheel.
The result of a line beam analysis shows that the maximum sagging moment occurs at 10.5m from the end of the deck under the leading wheel.
The axle will be positioned over the parapet beam as shown for Load case 1 to obtain the critical loading condition for bending in this member. This may also be the critical position for the design moment in the main edge beam, however the axle needs to be positioned as shown for Load case 2 to confirm the critical case.
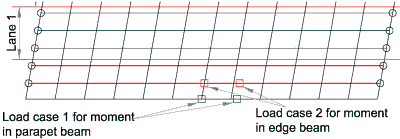
Other positions on adjacent transverse members need to be considered to take account of the skew effects.
As a check on the data, the total of the reactions should equal the total load of the axle = 200kN. Also the line beam analysis gives a total moment of 902.5kNm; so as there will be some distribution to adjacent members then the moment from the grillage should be in the order of (but less than) 900kNm in the longitudinal member.
Loads due to collision with parapets need to be considered in a grillage analysis in accordance with NA to BS EN 1991-2:2003 clause NA.2.30.1 and Table NA.6.
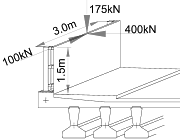
For very high containment metal parapets Class C loads are to be applied to the top of the parapet over a 3.0m length.
The point loads need to be transferred down to the datum level of the grillage, which is at the centroid of the deck slab, and distributed over a 3.0m length.
The high containment parapet is 1.5m high above the back of footpath level. The centroid of the deck slab is about 0.3m below the back of footpath level, consequently the two horizontal loads will induce moments on the grillage with a lever arm of 1.8m.
The 400kN horizontal load will produce a moment of 720kNm at the centre-line of the deck. This moment is distributed along a 3.0m length giving 240kNm/m moment to be applied to the grillage.
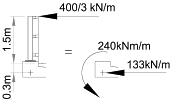
The horizontal load of 133kN/m will be taken into the deck which, as it is very stiff axially compared to bending, will distribute evenly between all longitudinal members and therefore have negligible effect in the grillage.
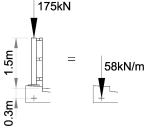
The 175kN vertical load can be idealised as a uniformly distributed load 58kN/m along a 3.0m length of the parapet beam.
The 100kN horizontal load acts in the plane of the parapet and there is an argument that the load will be resisted by the framing effect of the parapet rails with the posts and will therefore be transferred to the deck as a series of horizontal and vertical loads at the base of the posts.
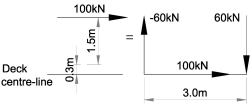
As the loads are to be applied over a 3.0m length then the moment of 100kN x (1.5 + 0.3) = 180kNm can be represented by a vertical couple of 60kN x 3.0m.
The horizontal load of 100kN will be taken into the deck which, as it is very stiff axially compared to bending, will distribute evenly between all longitudinal members and therefore have negligible effect in the grillage.
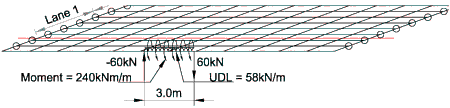
The three loads can be combined in one load case.
The 3.0m length can be positioned anywhere along the parapet beam and positions are generally chosen to coincide with the critical positions for the accidental wheel load.
The parapet collision load case acts together with 0.75 times the loading from LM1 and the Accidental Axle Load. It is convenient to obtain the effects from each load case separately rather than lump all the loads together in one load case. A combination case can then be used to sum the effects at the member you are considering.
Contact David Childs
David Childs
B.Sc, C.Eng, MICE
Last Updated: 28/01/2020