Combinations of Actions to UK National Annex
Index
1. Introduction
For the benefit of those who are making the transition from BS5400 to the Eurocodes
- dead loads become 'permanent actions' (Characteristic value = 'Gk')
- imposed loads, snow loads, thermal loads and wind loads are collectively called 'variable actions' (Characteristic value = 'Qk')
- load combinations become 'combinations of actions'.
In its simplest form a combination is Gk + Qk
For prestressed structures the effect of the prestressing action has been classified as a permanent action and identified separately by the variable P.
Thus the combination becomes Gk + P + Qk
The permanent actions Gk can comprise of several elements (weight of the beams and deck slab, weight of the parapets, weight of the road surfacing, weight of the footway construction, differential settlement, concrete shrinkage, etc.). Each of these elements are referenced by a suffix and given the variable letter 'j'.
Similarly the variable actions Qk can comprise of several elements (traffic loads, temperature effects, wind loads, snow loads, etc). Each of these elements are referenced by a suffix and given the variable letter 'i'.
The combination of all these different actions is ΣGk,j + P + ΣQk,i
The chance that the maximum design loading for each of the variable loads will occur all at the same time would be extremely unlikely during the 120 year design life of a bridge. Consequently the Eurocode sets out a series of reduction factors to enable realistic combinations to be used for design. Unless stated otherwise the variable action which produces the largest design load effect is identified (for road bridges this is usually one of the groups of traffic loads) and given the 'i' suffix 1 (i.e. Qk,1). This is called the 'leading variable action'. The other representative values of variable actions are reduced by a factor (ψ) and are defined as follows:
- The combination value (ψ0 Qk) of an action is intended to take account of the reduced probability of the simultaneous occurence of two or more variable actions.
- The frequent value (ψ1 Qk) is such that it should be exceeded for only a short period of time.
- The quasi-permanent value (ψ2 Qk) may be exceeded for a considerable period of time.
Tables NA.A2.1 and NA.A2.2 of the NA to BS EN 1990:2002+A1:2005 list values of ψ0, ψ1 and ψ2 for each type of variable action.
A summary of the design situations and the respective representative values which can be used at ultimate and serviceability limit states are shown in the table below:
Combination Factors for Appropriate Design Situations
Ultimate Limit State (ULS)
| Design Situation | Combination Value ψ0 |
Combination Value ψ1 |
Combination Value ψ2 |
| Persistent & Transient | Non- leading | — | — |
| Accidental | — | Leading | Leading & non- leading |
| Seismic | — | — | All variable actions |
| Design Situation | Comb. Value ψ0 | Comb. Value ψ1 | Comb. Value ψ2 |
| Persistent & Transient | Non- leading | — | — |
| Accidental | — | Leading | Leading & non- leading |
| Seismic | — | — | All variable actions |
Serviceability Limit State (SLS)
| Characteristic | Non- leading | — | — |
| Frequent | — | Leading | Leading & non- leading |
| Quasi- permanent | — | — | All variable actions |
| Characteristic | Non- leading | — | — |
| Frequent | — | Leading | Leading & non- leading |
| Quasi- permanent | — | — | All variable actions |
2. Serviceability Limit State
Serviceability limit states are concerned with the functioning of the structure
under normal use, the comfort of people, and the appearance of the
structure. Serviceability limit states may be reversible (e.g.
deflection) or irreversible (e.g. yield).
At SLS there are in principle three combinations of actions to consider:
- Characteristic ~ used for checking that no inelastic response occurs (allowable stresses are not exceeded)
- Frequent ~ used if deflection needs to be checked (this includes evaluation of dynamic response to ensure that users do not experience discomfort). Also used for decompression and crack width checks in prestressed concrete members.
- Quasi-permanent ~ this relates to long-term effects and is used for checking crack widths in concrete.
3. Ultimate Limit State
Ultimate limit states are concerned with the safety of people and the
structure. Examples of ultimate limit states include loss of equilibrium,
excessive deformation, rupture, loss of stability, transformation of the
structure into a mechanism, and fatigue.
Four Ultimate Limit States are considered in BS EN 1990, namely EQU, STR, GEO and FAT which are concerned with equilibrium, strength, ground and
fatigue.
For persistant and transient design situations under the STR limit state, the Eurocode defines three possible combinations which are given in expressions (6.10), (6.10a) and (6.10b).
However NA to BS EN 1990:2002+A1 Clause NA.2.3.7.1 A2.3.1(1) says that for the design of bridges the combination of actions should be based on equation 6.10.
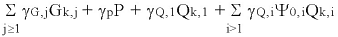 ............ (6:10)
............ (6:10)
The leading variable action Qk,1 is multiplied by its appropriate safety factor γQ,1 .
Other variable actions Qk,i , for i>
1, which may act simultaneously with the leading variable
action Qk,1, are taken into account as accompanying variable
actions and are represented by their combination value, i.e.
their characteristic value reduced by the relevant combination
factor Ψ0, and are multiplied by the appropriate safety factor γQ to
obtain the design values.
The appropriate safety factors γQ are obtained from NA to BS EN 1990:2002+A1 Tables NA.A2.4(A to C) & 5 as follows:
- Static equilibrium (EQU) should be verified using Table NA.A2.4(A).
- Design of structural members (STR) not involving geotechnical actions should be verified using Table NA.A2.4(B).
- Design of structural members (STR) involving geotechnical actions and the resistance of the ground (abutments, wing walls, piers etc.) should be verified using Tables NA.A2.4(B) & NA.A2.4(C) using Approach 1.
- γ = 1.0 for the design values of actions given in Table NA.A2.5
Contact David Childs