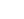Reinforced Concrete Deck Example to Eurocodes
Reinforced Concrete Deck Design to EN 1992-2 & UK National Annex
Problem:
Design a simply supported reinforced concrete deck slab using a unit strip method. The deck carries a 100mm depth of surfacing, together with a traffic load (LM1) udl of 5.5 kN/m2 and tandem axle load of 100kN (300kN/3m lane width). The deck should also be designed to carry the SV80 model vehicle. The span of the deck is 12.0m centre to centre of bearings.
γconc. = 25kN/m3
SV80 model vehicle also to be considered.
Use C32/40 concrete to BS 8500.
Use Grade B500B reinforcement to BS 4449.
A Solution:
EN 1992-1-1 Table 4.1 gives the Exposure Class XD1 as suitable for deck soffits.
NA to BS EN 1992-1-1 clause 4.4.1.2(5) says values of cmin,dur shall be taken from BS 8500-1
BS 8500-1 Table A.5
Nominal cover for C32/40 concrete = cnom = cmin,dur + Δcdev = 45 + Δcdev with
maximum water-cement ratio = 0.55 and minimum cement content of 320 kg/m3
Fixing tolerence for reinforcement Δcdev = 15mm for insitu concrete
∴ Nominal cover cnom = 45 + 15 = 60mm
Loading
Design for a 1 metre width of deck (unit strip)
Note: The loading has been simplified to demonstrate the method of designing the slab
(See BS EN 1991-1-1 to 1991-1-7, 1991-2 and National Annex for full design loading.)
EN 1991-1-1 Annex A
Permanent Actions (Gk):
deck slab = 25 × 0.65 × 1.0 = 16.3 kN/m
NA Table NA.1 cl. 5.2.3(3)
It will be assumed that the depth of surfacing could vary considerably as a result of future resurfacing. Clause 5.2.3(3) makes an allowance of up to 55% additional weight.
surfacing = 1.55 × 24 × 0.1 × 1.0 = 3.7 kN/m
EN 1991-2
Table 4.2
Variable Actions (Qk):
Traffic Load Model 1 (Q1k = 1 & q1k = 0.61)
= 5.5 kN/m(udl) + 2 × (300kN/3m) axles @ 1.2m centres.
NA Fig NA.1
Traffic Load Model 3 (SV80)
= 6 × (130kN/3m) axles @ 1.2m c/c
NA Cl. 2.16.3
DAF for 130kN axle = 1.16 ∴ axle load = 1.16×130/3 = 50.3kN
Combination of Actions
a) Ultimate Limit State : EN 1990 clause 6.4.3.2 requires one combination of actions to be considered for the "STR" limit state:
Eqn 6.10
Ed = E(ΣγGjGkj + γpP + γQ,1Qk,1 + ΣγQ,iΨ0,iQk,i)
Table NA.A.2.4
Group of Loads
γsup
γinf
Ψ0
Dead Load
1.35
0.95
-
Superimposed Dead Load
1.20
0.95
-
Temperature Difference
1.55
0
0†
Traffic Groups
1.35
0
N/A‡
Key:
† EN 1990 Table A.2.1 Note 3 says the value of Ψ0 of 0.6 may be reduced to 0 when considering ULS.
‡ Traffic loads are the leading action
b) Serviceability Limit State : EN 1990 clause 6.5.3 requires three combinations of actions to be considered for the serviceability limit state:
- Characteristic combination Ed = E(ΣGkj + P + Qk,1 + ΣΨ0,iQk,i) for limiting stresses
- Frequent combination Ed = E(ΣGkj + P + Ψ1,1Qk,1 + ΣΨ2,iQk,i)
- Quasi-permanent combination Ed = E(ΣGkj + P + ΣΨ2,iQk,i) for crack control
Table NA.A.2.1
Action
Ψ0
Ψ1
Ψ2
Traffic load group gr1a
0.75
0.75
0
Traffic load group gr5
0
0
0
Thermal
0.6
0.6
0.5
Temperature Difference Effects
Apply temperature differences given in EN 1991-1-5 Figure 6.2c(Type 3a) to a 1m wide deck section.
EN 1991-1-5 Table C.1 - Coefficient of thermal expansion = 10 × 10-6 per °C.
CIRIA Report C660 ("Early-age thermal crack control in concrete") suggests that a value of 10 × 10-6 per °C is unsuitable for some of the concrete aggregates used in the UK and suggest a value of 12 × 10-6 per °C should be used if the type of aggregate has not been specified.
∴ use 12 × 10-6 per °C
From EN 1992-1-1 Table 3.1 :
fck = 32 → fcm = fck +8 = 40 → Ecm = 22[(fcm) / 10]0.3 = 22 × 40.3 = 33.35 kN/mm2
Hence restrained temperature stresses per °C = 33.35 × 103 × 12 × 10-6 = 0.4 N/mm2
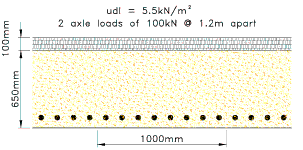
Interpolating values of ΔT from EN 1991-1-5 Table B.3 for a 0.65m depth of slab with 100mm surfacing we get:
Section Properties
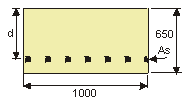
Area = 1000 × 650 = 0.65 × 106 mm2
Second Moment of Area = 1000 × 6503 / 12 = 22.9 × 109 mm4
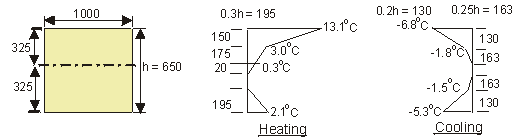
a) Heating temperature difference
Force F to restrain temperature strain :
0.4 × 103 × [ 150 × ( 3.0 + 5.05 ) + (195 × 1.5) + (195 × 1.05)] × 10-3 = 683 kN
Moment M about centroid of section to restrain
curvature due to temperature strain :
0.4 × 103 × [150 × (3.0 × 250 + 5.05 × 275) + 175 × (0.3 × 87.5 + 1.35 × 116.7) - (20 × 0.15 × 6.7) - (195 × 1.05 × 260)] × 10-6 = 119.9kNm
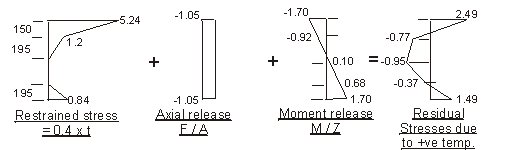
b) Cooling temperature difference
Force F to restrain temperature strain :
- 0.4 × 103 × [ 130 × ( 1.8 + 2.5 + 1.5 + 1.9 ) + 163 × ( 0.9 + 0.75 )] × 10-3 = - 508 kN
Moment M about centroid of section to restrain
curvature due to temperature strain :
- 0.4 × 103 × [130 × ( 1.8 × 260 + 2.5 × 282 - 1.5 × 260 - 1.9 × 282 ) +
163 × ( 0.9 × 141 - 0.75 × 141 )] × 10-6 = -14.3kNm
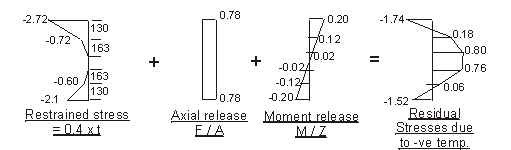
Note:
1) Sign convention is compressive stresses are positive.
2) The deck is simply supported and allowed to expand and contract freely. Therefore there will be no secondary stresses due to the curvature and axial strain in the deck.
Dead + Superimposed Dead Loading (per metre width of deck)
SLS = Serviceability Limit State
ULS = Ultimate Limit State
Design SLS moment = ∑Gkj = (16.3 + 3.7) × 122 / 8 = 360 kNm
Design ULS moment = ∑(γGjGkj) = [(1.35 × 16.3) + (1.2 × 3.7)] × 122 / 8] = 476 kNm
Variable Actions (per metre width of deck)
Traffic Group gr1a
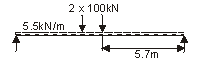
Footway loading will not affect the unit strip loading.
Moment at leading axle = 5.5 × (6 × 6.3 - 6.32/2) + 100 × 5.7 × (6.3 + 5.1) / 12 = 640 kNm
Design SLS moment characteristic combination = Qk1 = 640 kNm
Design ULS moment = γQ1Qk1 = 1.35 × 640 = 864 kNm
Traffic Group gr5
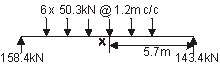
Model LM1 is positioned 5m clear of LM3 and will be off the deck.
Moment at X = 143.4 × 5.7 - 50.3 × (2.4 + 1.2) = 636kNm
Design SLS moment characteristic combination = Qk1 = 636 < 640 kNm
∴ gr1a governs
Design ULS moment = γQ1Qk1 = 1.35 × 636 = 859 < 864 kNm
∴ gr1a governs
Combinations of Actions
a) Ultimate Limit State
Ed = E(ΣγGjGkj + γpP + γQ,1Qk,1 + ΣγQ,iΨ0,iQk,i)
Design ULS mid span moment = 476 + 0 + 864 + 0 = 1340 kNm
b) Serviceability Limit State
Characteristic Combination
Ed = E(ΣGkj + P + Qk,1 + ΣΨ0,iQk,i)
Design SLS mid span moment:
= 360 + 0 + 640 + 0.6 × (differential temperature effects)
= 1000 kNm + 0.6 × (differential temperature effects)
Quasi-permanent Combination
Ed = E(ΣGkj + P + ΣΨ2,iQk,i)
Design SLS mid span moment = 360 + 0 + 0.5 × 0 = 360 kNm
Ultimate Capacity of Deck Slab
Ultimate Design Moment = 1340 kNm
EN 1992-1-1 & EN 1992-2
It is usual to design reinforced concrete for the ultimate limit state and check for serviceability conditions.
cl. 3.1.6(101)P
Design compressive strength = fcd = αccfck / γc
cl. 3.1.7
αcc = 0.85
cl. 2.4.2.4
Table 2.1N: γc = 1.5, γs = 1.15
fcd = 0.85 × 32 / 1.5 = 18.1 N/mm2
Table 3.1
εc2 = 0.002, εcu2 = 0.0035, n = 2.0
Try 32mm dia. reinforcement at 125mm centres:
Nominal cover to reinforcement in deck soffit = 60mm
Fig. 3.3
Using parabolic-rectangular diagram:
Average stress fav = fcd[1-εc2 / {εcu2(n+1)}] = 18.1 × [1 - 0.002 / {0.0035 × (2 + 1)}] = 14.7 N/mm2
Assuming steel yields then:
M = fsz = fykAsz / γs = Fcz = favbXz
Depth to neutral axis X = fykAs / (favbγs)
X = 500 × 6434 / (14.7 × 1000 × 1.15) = 190.6mm
Check that steel will yield:
Cl. 3.2.7(4)
Modulus of Elasticity Es = 200 kN/mm2
Steel strain at yield = εs,yield = fyk / γs / Es = 500 / 1.15 / 200000 = 0.00217
from linear strain relationship:
εs = εcu2(d/X - 1) = 0.0035 ( 574 / 190.6 - 1) = 0.007 > 0.00217 ∴ steel will yield.
Hence Mult = favbXz = favbX(d - βX)
Where β = 1 - [0.5εcu22 - εc22 / {(n+1)(n+2)}] / [εcu22 - εcu2εc2 / (n+1)]
β = 1 - [0.5 × 0.00352 - 0.0022 / {(2 + 1) × (2 + 2)}] / [0.00352 - 0.0035 × 0.002 / (2 + 1)] = 0.416
Mult = 14.7 × 1000 × 190.6 × (574 - 0.416 × 190.6) × 10-6 = 1386 kNm > 1340 ∴ OK
Check Serviceability Limit State
Characteristic Combination SLS Design Moment = 1000 kNm (360 + 640) + 0.6 × (differential temperature effects)
Check stresses in the concrete and reinforcement at:
i) Early Age (before creep has occurred)
ii) Long term after all the creep has taken place.
i) Before creep has occurred the cracked section properties will be based on the short-term modulus for all actions.
EN 1992-1-1 Table 3.1
Ecm = 22[(fck + 8) / 10]0.3 = 22[(32 + 8) / 10]0.3 = 33.4 kN/mm2
Ec,eff = Ecm = 33.4 kN/mm2
Modular Ratio m = Es / Ecm = 200 / 33.4 = 6.0
Let dc = depth to neutral axis then equating strains for cracked section:
εs = εc(d - dc) / dc
Equating forces:
AsEsεs = 0.5bdcεcEc,eff
Hence dc = [-AsEs + {(AsEs)2 + 2bAsEsEc,effd}0.5] / bEc,eff
dc = [-6434 × 200000 + {(6434 × 200000)2 + 2 × 1000 × 6434 × 200000 × 33400 × 574}0.5] / (1000 × 33400) = 175mm
Cracked second moment of area = As(d-dc)2 + Ec,effbdc3 / 3Es
INA = 6434 × (574 - 175)2 + 33.4 × 1000 × 1753 / (3 × 200) = 1.32 × 109 mm4 (steel units)
Concrete stress σc = M / zc + 0.6 × (differential temperature effects)
σc = {1000 × 106 × 175 / (1.32 × 109 × 6.0)} + (0.6 × 2.49) = 22.1 + 1.5 = 23.6 N/mm2 (Heating temperature difference)
cl. 7.2(102)
Limiting concrete stress = k1fck
k1 = 0.6
Limiting concrete stress = 0.6 × 32 = 19.2 N/mm2 < 23.6 ∴ Fail
The concrete strength class will need to be increased to class C40/50
Re-working the example gives:
Ecm = 35.2 kN/mm2 m = 5.7 dc = 171 mm INA = 1.34 × 109 mm4
σc = 22.4 + 1.5 = 23.9 N/mm2
Limiting stress = 0.6 × 40 = 24 N/mm2 > 23.9 ∴ OK
EN 1992-1-1
ii) After all creep has taken place the cracked section properties will be based on the long-term and short-term modulus for the various actions.
Short-term modulus = Ecm
Long-term modulus = Ecm / (1+φ)
Effective modulus Ec,eff = (Mqp + Mst)Ecm / {Mst + (1 + φ)Mqp}
Table 3.1
fcm = fck + 8 = 40 + 8 = 48 N/mm2
Cl. 3.1.4
Relative humidity of the ambient environment = 80% (outside conditions)
Age of concrete at initial loading t0 = 6 days (when soffit formwork is released)
Annex B (B.6)&(B.8c)
h0 = 650
α1 = [35 / fcm]0.7 = [35 / 48]0.7 = 0.80
α2 = [35 / fcm]0.2 = [35 / 48]0.2 = 0.94
(B.3b)
φRH = [1 + α1 × {(1 - RH / 100) / (0.1 × h01/3)}] × α2
φRH = [1 + 0.8 × {(1 - 80 / 100) / ( 0.1 × 6501/3)}] × 0.94 = 1.113
(B.4)
β(fcm) = 16.8 / fcm0.5 = 16.8 / 480.5 = 2.425
(B.5)
β(t0) = 1 / (0.1 + t00.2) = 1 / ( 0.1 + 60.2) = 0.653
(B.2)
φ0 = φRH × β(fcm) × β(t0) = 1.113 × 2.425 × 0.653 = 1.762
Moment due to long-term actions = Mqp = 360 kNm
Moment due to short-term actions = Mst = 640 kNm
Hence Effective Modulus Ec,eff = {(360 + 640) × 35.2} / {640 + 360 × ( 1 + 1.762)} = 21.5 kN/mm2
Modular Ratio m = Es / Ec,eff = 200 / 21.5 = 9.3
Let dc = depth to neutral axis then equating strains for cracked section:
εs = εc(d - dc) / dc
Equating forces:
AsEsεs = 0.5bdcεcEc,eff
Hence dc = [-AsEs + {(AsEs)2 + 2bAsEsEc,effd}0.5] / bEc,eff
dc = [-6434 × 200000 + {(6434 × 200000)2 + 2 × 1000 × 6434 × 200000 × 21500 × 574}0.5] / (1000 × 21500) = 209mm
Cracked second moment of area = As(d-dc)2 + Ec,effbdc3 / 3Es
INA = 6434 × (574 - 209)2 + 21.5 × 1000 × 2093 / (3 × 200) = 1.18 × 109 mm4 (steel units)
Concrete stress σc = M / zc + 0.6 × (differential temperature effects)
σc = {1000 × 106 × 209 / (1.18 × 109 × 9.3)} + (0.6 × 2.49) = 19.1 + 1.5 = 20.6 N/mm2 (Heating temperature difference)
cl. 7.2(102)
Limiting concrete stress = k1fck
k1 = 0.6
Limiting concrete stress = 0.6 × 40 = 24.0 N/mm2 > 20.6 ∴ OK
cl. 7.2(5)
Limiting steel stress = k3fyk
k3 = 0.8
Limiting steel stress = 0.8 × 500 = 400 N/mm2
Tensile stress due to cooling temperature difference =
9.3 × [{(1.52 + 0.06) × (130 - 60 - 16) / 130} - 0.06] = 5.5 N/mm2
Steel stress σs = M / zs + 0.6 × (differential temperature effects)
σs = {1000 × 106 × (574 - 209) / (1.18 × 109)} + (0.6 × 5.5) = 309 + 3
σs = 312 N/mm2 < 400 ∴ OK
Crack Control:
Consider worst condition before creep has occurred and
Quasi-Permanent Combination Moment = 360 kNm (no secondary effects from temperature difference as deck is simply supported single span)
Cl. 7.3.4(1)
Crack width wk = sr,max(εsm - εcm)
Cl. 7.3.4(3)
Spacing Limit = 5(c+φ/2) = 5(60 + 32/2) = 380mm > 125mm ∴ OK
sr,max = k3c + k1k2k4φ / ρp,eff
k1 = 0.8 (high bond bars)
k2 = 0.5 (for bending)
k3 = 3.4 (recommended value)
k4 = 0.425 (recommended value)
Cl. 7.3.2(3)
hc,eff is the lesser of:
i) 2.5(h-d) = 2.5(650 - 574) = 190
ii) (h-x)/3 = (650 - 175) / 3 = 158
iii) h/2 = 650 / 2 = 325
∴ hc,eff = 158 mm
and Ac,eff = 158 × 1000 = 158000 mm2
Cl. 7.3.4(2)
ρp,eff = As / Ac,eff = 6434 / 158000 = 0.0407
sr,max = k3c + k1k2k4φ / ρp,eff
sr,max = (3.4 × 60) + (0.8 × 0.5 × 0.425 × 32) / 0.0407 = 204 + 134 = 338
Cl. 7.3.4(2)
(εsm - εcm) = [σs - {ktfct,eff(1 + αeρp,eff) /ρp,eff}] / Es ≥ 0.6σs / Es
kt = 0.4 for permanent loading (no short-term loading included in design moment of 360 kNm)
αe = Es / Ecm = 200 / 35.2 = 5.7
σs = 360 × 106 × (574 - 171) / (1.34 × 109) = 108 N/mm2
Table 3.1
fct,eff = fctm = 3.5 N/mm2
(εsm - εcm) = [108 - {0.4 × 3.5 × (1 + 5.7 × 0.0407) / 0.0407}] / 200000 = 0.328 × 10-3
0.6σs / Es = 0.6 × 108 / 200000 = 0.324 × 10-3 < 0.328 × 10-3 ∴ OK
Crack width wk = sr,max(εsm - εcm) = 338 × 0.328 × 10-3 = 0.11 mm
NA EN 1992-2 Table NA.2
Recommended value of wmax = 0.3 mm > 0.11 mm ∴ OK
Hence B32 bars at 125 centres are adequate for the mid span. The concrete strength class will need to be C40/50
Shear Design
Shear is designed for ultimate limit state.
cl. 5.4.4
VEd = shear force due to ultimate actions.
Maximum VEd due to permanent actions = Σ(γGjGkj)
VEd = [(1.35 × 16.3) + (1.2 × 3.7)] × 12 / 2 = 159 kN
Traffic Group gr1a

Cl. 6.2.2(6)
Reduction factor β for tandem axle at support = av / 2d = 0.5d / 2d = 0.25
Minimum reduction is applied at 2d = 2 × 0.574 = 1.148m from support
Only one axle should be considered for reduced load effect (see PD 6687-2:2008 Cl. 7.2.2)
Maximum VEd due to gr1a = Σ(γQ1Qk1) = 1.35 × [100 × (0.25 + 10.8/ 12) + (5.5 × 6.0)] = 188 kN
Traffic Group gr5
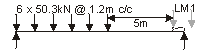
TS axles of LM1 are not fully on the deck ∴ ignore the load effects from these axles [see EN 1991-2 Clause 4.3.2(1a)]
Cl. 6.2.2(6)
Reduction factor β for axle at support = av / 2d = 0.5d / 2d = 0.25
Minimum reduction is applied at 2d = 2 × 0.574 = 1.148m from support
Only one axle should be considered for reduced load effect (see PD 6687-2:2008 Cl. 7.2.2)
Maximum VEd due to gr5 = Σ(γQ1Qk1) = 1.35 × {50.3 × [0.25 + (10.8 + 9.6 + 8.4 + 7.2 + 6) / 12] + 5.5 × 1.0 × 0.5 / 12} = 255 kN
Maximum VEd from variable actions is from traffic group gr5 = 255 kN
Maximum Combination VEd = Σ(γGjGkj + γQ1Qk1) = 159 + 255 = 414 kN
Cl. 6.2.2(101)
Shear Capacity of Slab: Try B32 dia. reinforcement @ 125c/c
VRd,c = [CRd,ck(100ρ1fck)1/3]bwd
CRd,c = 0.18 / γc = 0.18 / 1.5 = 0.12
k = 1 + (200 / d)0.5 ≤2.0
k = 1 + (200 / 574)0.5 = 1.59 < 2.0
ρ1 = Asl / bwd ≤0.02
ρ1 = 6434 / (1000 × 574) = 0.011 < 0.02
Cl. 3.1.2(102)P
fck = 40 ( < Cmax = C50/60)
VRd,c = [0.12 × 1.59 × (100 × 0.011 × 40)1/3] × 1000 × 574 × 10-3 = 387 kN ( < 414 kN Fail : see below)
Minimum VRd,c = (vmin)bwd = 0.035k3/2fck1/2bwd = 0.035 × 1.593/2 × 401/2 × 1000 × 574 × 10-3 = 255 kN
cl 6.2.2(6)
Check that the maximum allowable shear force is not exceeded:
Maximum allowable shear force = 0.5bwdνfcd
ν = 0.6[1 - fck / 250] = 0.6 × [1 - 40 / 250] = 0.504
fcd = αccfck/γc
αcc = 1.0 [see NA to Cl. 3.1.6(101)P]
fcd = 1.0 × 40 / 1.5 = 26.7 N/mm2
Maximu VEd = 0.5 × 1000 × 574 × 0.504 × 26.7 × 10-3 = 3857 kN >> 414 kN
VRd,c = 387 kN < VEd = 414 kN ∴ Fail. It would be necessary to increase the longitudinal reinforcement to B40 at 125 c/c however the UK National Annex allows an alternative approach.
NA to 1992-2 Cl. 6.2.2(101)
Alternative Solution:
If the reduction factor β is not used to reduce the applied shear force actions then the allowable shear force VRd,c may be enhanced if the section being considered is within 2d of the support.
Traffic Group gr5
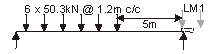
Ignore effects from LM1
i) Consider a section at d (a = 0.574m) from the support :
Maximum ULS shear force due to gr5 = 1.35 × [50.3 × (11.426 + 10.226 + 9.026 + 7.826 + 6.626 + 5.426)/12] = 286 kN
Maximum VEd from permanent actions = {[(1.35 × 16.3) + (1.2 × 3.7)] × 12/2} - {0.574 × [(1.35 × 16.3) + (1.2 × 3.7)]} = 143 kN
Maximum Combination VEd = Σ(γGjGkj + γQ1Qk1) = 143 + 286 = 429 kN
Enhanced CRd,c = (0.18/γc) × (2d/a) = (0.18 / 1.5) × 2 = 0.24
VRd,c = [CRd,ck(100ρ1fck)1/3]bwd
VRd,c = [0.24 × 1.59 × (100 × 0.011 × 40)1/3] × 1000 × 574 × 10-3 = 773 kN ( > 429 kN ∴ OK)
ii) Consider a section at 2d (a = 1.148m say 1.15m) from the support (no enhancement):
Maximum ULS shear force due to gr5 = 1.35 × [50.3 × (10.85 + 9.65 + 8.45 + 7.25 + 6.05 + 4.85) / 12] = 267 kN
Maximum VEd from permanent actions = {[(1.35 × 16.3) + (1.2 × 3.7)] × 12/2} - {1.15 × [(1.35 × 16.3) + (1.2 × 3.7)]} = 128 kN
Maximum Combination VEd = Σ(γGjGkj + γQ1Qk1) = 128 + 267 = 395 kN
VRd,c = 387 kN ≈ 395 kN (2% error say OK for conservative nature of unit strip analysis)
Hence B32 bars at 125 centres are adequate for shear at the ends of the deck.
Note: Intermediate sections between mid span and the ends of the deck will have a smaller moment than at mid span and a small shear than at the ends of the deck. These sections need to be checked to determine where the reinforcement may be reduced to B25 at 125c/c.
cl. 7.3.2(2)
Minimum area of reinforcement As,min = kckfct,effAct / σct
kc = 0.4
k = 1.0 - {[(h - 300) / (800 - 300)] × (1.0 - 0.65)} = 0.755
Table 3.1
fct,eff = fctm = 3.5 N/mm2
Act = 1000 × 650 / 2 = 325000 mm2
σs = fyk = 500 N/mm2
As,min = 0.4 × 0.755 × 3.5 × 325000 / 500 = 687 mm2
cl. 9.2.1.1(1)
Minimum area of longitudinal reinforcement As,min = 0.26btdfctm / fyk > 0.0013btd
As,min = 0.26 × 1000 × 574 × 3.5 / 500 = 1045 mm2
0.0013btd = 0.0013 × 1000 × 574 = 746 > 1045 ∴ OK
Hence minimum longitudinal steel (bottom of slab) = B16 @ 125 c/c (As = 1608 mm2 > 1045)
Minimum distribution steel = B12 @ 125 c/c longitudinally (As = 905 mm2 > 687) & B12 @ 150 c/c transversely (As = 754 mm2 > 687)
Contact David Childs