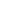Reinforced Concrete to BS EN 1992-2 & UK National Annex
Index
1. Introduction
Both the Serviceability and Ultimate Limit States need to be considered.
Serviceability Limit State ensures that crack widths do not exceed specified values, and also ensures that concrete and reinforcement stresses are maintained below a safe limit.
Ultimate Limit State ensures that the structure will not collapse.
2. Serviceability Limit State
i) Crack Control
Cracks in concrete can be caused by :
- corrosion of the reinforcement which causes the concrete to spall
- thermal movements, particularly cooling from heat of hydration (called early thermal cracking)
- structural actions such as bending, shear or torsion
Corrosion of reinforcement is controlled by use of suitable concrete grades and providing adequate cover to the reinforcement.
Cracks due to thermal movements are controlled by providing minimum nominal steel area and restricting the maximum bar spacing. Ciria Publication C660 is used to calculate the minimum steel area and bar spacing to control early thermal cracking.
The width of shear cracks is controlled by ultimate strength calculations.
Crack widths caused by bending and tension may be calculated using Clause 7.3.4, alternatively Clause 7.3.3 may be used to limit the stress in the bar for a given bar diameter, or a given bar spacing, from
Tables 7.2N & 7.3N.
For calculating the crack width only the quasi-permanent load combination is used.
ψ2 = 0 for traffic actions and ψ2 = 0.5 for thermal actions consequently only thermal actions (variable action) are considered in combination with the permanent actions. However only secondary effects of the temperature difference need to be considered; the primary self-equilibrating stresses may be ignored.
Crack widths may be calculated using Clause 7.3.4. The crack width (wk) is a function of the spacing between the cracks (sr,max) and the strain in the reinforcement (εsm) and concrete (εcm):
wk = sr,max(εsm - εcm) ... ....Equation (7.8)
where sr,max = k3c + k1k2k4φ/ρp,eff .... ...Equation (7.11)
and (εsm - εcm) = {σs - [ktfct,eff(1 + αeρp,eff)/ρp,eff]}/Es ≥ 0.6σs/Es .... ...Equation (7.9)
Using a rectangular section as an example:
We first need to determine the position of the neutral axis:
Es = 200kN/mm2 (clause 3.2.7(4))
The short-term value of Ec,eff is obtained from the value of Ecm in Table 3.1 which is appropriate to the live load portion of the moment (Mst). The permanent load portion of the moment (Mqp) has a long-term value of Ec,eff to take account of the effects of creep. The modified value of Ec,eff used for the crack width calculation is an intermediate value between the short and long term values.
Modified Ec,eff = Ecm(Mst + Mqp) / [Mst + Mqp(1 + φ)] where φ is the value of the creep coefficient φ(∞,t0).
αeff = Modular ratio = Es / Ec,eff.
ρp,eff = As / bd and ρ'p,eff = A's / bd
Then
x/d = √{[αeffρp,eff+(αeff-1)ρ'p,eff]2+2[αeffρp,eff+(αeff-1)ρ'p,effd'/d]}-[αeffρp,eff+(αeff-1)ρ'p,eff]
Second Moment of Area of Cracked Section Ic = bx3/3 + (αeff-1)As'(x-d')2 + αeffAs(d-x)2
Hence reinforcement stress σs = αeffMEd(d-x)/Ic where MEd = Mqp+Mst
kt is obtained by interpolation between 0.4 for long-term and 0.6 for short-term loadings:
kt = 0.4 + (0.2Mst/MEd)
fct,eff = fctm (from Table 3.1)
αe = αeff = Es / Ec,eff
ρp,eff = (As + ξ1A'p)/Ac,eff where A'p = 0
Ac,eff = bhc,ef where hc,ef is the lesser of 2.5(h-d), (h-x)/3 or h/2
(εsm - εcm) can now be evaluated from Equation (7.9)
sr,max can also be evaluated from Equation (7.11) with:
k1 = 0.8 (for high bond reinforcement)
k2 = 0.5 (for bending)
k3 = 3.4 and k4 = 0.425 (from UK National Annex to EN 1992-1-1)
The Crack Width wk can now be calculated using Equation (7.8) in clause 7.3.4(1)
ii) Stress Limits
The methods given in the code for checking crack widths assumes a linear elastic behaviour. It is therefore necessary to check the stress limits to ensure this assumption is correct. in particular that the strains caused by transient loads will not become permanent.
The section properties are determined by considering whether the concrete in the tension zone is cracked or not. This is done by assuming initially that the section is uncracked whereby the second moment of area of the section Ic is for the full concrete section (bh3/12 for a rectangular section).
The maximum tensile stress in the concrete is obtained from MEd y / Ic and compared with the tensile strength of the concrete fctm from Table 3.1.
If the tensile stress is greater than fctm then the section will be considered cracked and the stresses calculated using a cracked elastic section analysis similar to that used to determine the crack width described above.
All load combinations need to be checked to ensure that the stress limits are not exceeded.
As the maximum design variable loading can occur at any time during the life of the bridge then, for the cracked section, it is usual to check the stresses at first opening and also after all the creep has occurred at the end of the life of the bridge. This is done by using Ec,eff = Ecm for both the short and long-term loading when the bridge is first opened, and using the modified value of Ec,eff, as described in the crack control calculation above, for the full life of the bridge.
The stress limits given in the code are:
k3fyk = 0.8fyk for reinforcement in tension (BS EN 1992-1-1:2004 Clause 7.2.(5)).
k1fck = 0.6fck for concrete in compression (BS EN 1992-2:2005 Clause 7.2.(102)).
3. Ultimate Limit State
To determine the moment of resistance of a member at failure by limit state analysis the following assumptions are made:
- The distribution of strain across any section is linear. This means that plane sections before bending remain plane after bending, and the strain at any point is proportional to its distance from the neutral axis.
- The resistance of concrete in tension is ignored.
- The relationship between the stress and strain in the reinforcement is as shown in Figure 3.8 of EN 1992-1-1 with γs = 1.15.
- The relationship between the stress and strain in the concrete is as shown in Figure 3.4 of EN 1992-1-1 with fcd = αccfck/γc ( αcc = 0.85, γc = 1.5). The distribution of stress in the concrete at failure may be represented by a uniform stress fav = ηfcd acting over the depth of the compression zone λX where X is the depth to the neutral axis.
Clause 3.1.7(3) of EN 1992-1-1 allows a rectangular concrete stress distribution to be assumed as shown below. The value of λ = 0.8 for fck ≤ 50 MPa, and λ = 0.8-(fck-50)/400 for 50 < fck ≤ 90 MPa.
The value of the uniform stress fav = ηfcd where η = 1.0 for fck ≤ 50 MPa, and η = 1.0-(fck-50)/200 for 50 < fck ≤ 90 MPa.
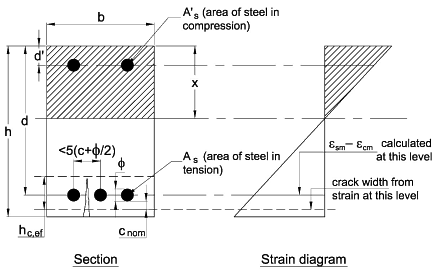
For the singly reinforced rectangular section (assuming the reinforcement yields):
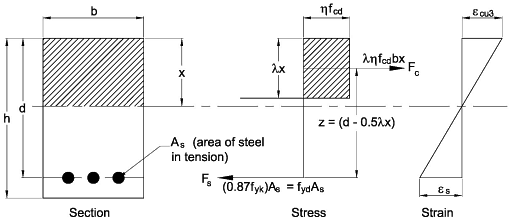
Taking moments about the centre of compression for the tensile force
Mu = fydAsz = 0.87fykAsz
The depth to the neutral axis depends upon the reinforcement provided and is obtained by equating the forces:
Fs = Fc → 0.87fykAs = 0.85ληfckbx/1.5
Rearranging and dividing both sides by d we get:
(x/d) = (1.53fykAs) / (ληfckbd)
Lever arm z = (d - 0.5λx) so substituting for x we get:
z = (1 - [0.77fykAs] / [ηfckbd])d
To meet the criteria for assuming the reinforcement yields then the strain in the steel εs needs to be greater than εs,yield.
From the strain diagram εs = εcu3(d-x)/x which has to be greater than 0.87fyk/Es
This re-arranges to x/d ≤ 1 / {[0.87fyk/(Esεcu3)]+1} ... Equation(A)
If x/d does not meet this condition then the options are:
- calculate the actual force in the reinforcement using the strain compatibility method and hence the moment of resistance, or
- increase d, or
- increase the concrete strength or add compression reinforcement.
For the doubly reinforced rectangular section:
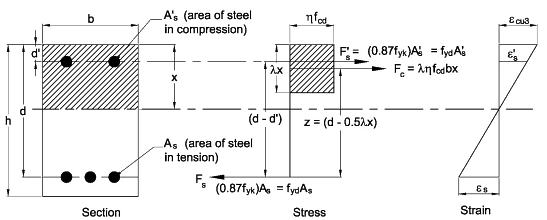
Equating the tensile and compressive forces
Fs = Fc + F's → 0.87fykAs = 0.85ληfckbx/1.5 + 0.87fykA's
0.87fyk(As - A's) = 0.57ληfckbx ... Equation(B)
If compression reinforcement needs to added as for option (3) in the singly reinforced section above then the procedure is:
- reduce x in equation (A) so that it satisfies the equation
- provide compression reinforcement A's , by re-arranging equation (B)
A's = As - 0.65ληfckbx/fyk
If both As and A's are known then equation (B) can be re-arranged to determine x:
x = 1.53fyk(As - A's) / (ληfckb)
To meet the criteria for assuming the reinforcement yields then the tension reinforcement can be checked using equation (A).
To ensure the compression reinforcement yields then the strain in the steel ε's needs to be greater than εs,yield.
From the strain diagram ε's = εcu3(1-d'/x) which has to be greater than 0.87fyk/Es
This re-arranges to x/d' ≤ 1 / {1 - [0.87fyk/(Esεcu3)]}.
If either of these checks fails then the ultimate moment of resistance needs to be determined using the strain compatibility method.
4. Shear
a) Members Without Shear Reinforcement
Tests have been carried out on beams with and without shear reinforcement. The results for members without shear reinforcement show a correlation between the concrete strength, the amount of longitudinal tension reinforcement and the depth of the section.
The shear strength (VRd,c) of a section without shear reinforcement is give by:
VRd,c = [CRd,ck(100ρ1fck)1/3 + k1σcp]bwd (BS EN 1992-2 Clause 6.2.2(101))
with a minimum value of VRd,c = (vmin + k1σcp)bwd
where:
CRd,c = 0.18/γc (UK NA to BS EN 1992-2 Clause 6.2.2(101))
k = 1 + √(200/d) ≤2.0
ρ1 = Asl / bwd ≤0.02
Asl = Area of longitudinal tensile reinforcement at effective depth d
bw = smallest width of section in the tension zone
fck = concrete cylinder strength (limited to C50 ~ see UK NA to BS EN 1992-2 Clause 3.1.2(102)P)
k1 = 0.15 (UK NA to EN 1992-2 Clause 6.2.2(101))
σcp = NEd / Ac (N/mm2)
NEd = Axial force from any applied loading
Ac = Gross concrete area
vmin = 0.035k3/2fck1/2
Note: For sections close to supports the UK National Annex to BS EN 1992-2 Clause 6.2.2(101) allows the value of CRd,c to be increased to (0.18/γc)•(2d/a) provided that the shear force VEd is not
multiplied by β (see EN 1992-1-1 Clause 6.2.2 (6)) and the longitudinal reinforcement is fully anchored at the support, where 'a' is the distance from the edge of the support (or centre of bearing where flexible bearings are used) to the position at which the shear resistance is considered.
It is convenient not to put shear links in concrete slabs and if VRd,c is found to be insufficient then it is usually more efficient to provide additional longitudinal tension reinforcement.
Beams, however, have to be provided with shear links even if VRd,c is found to be adequate. BS EN 1992-1-1 Clause 9.2.2(5) says:
the minimum shear reinfrocement ratio ρw,min = Asw / (s.bw.sinα) = (0.08√fck) / fyk
Clause 9.2.2(6) says the spacing (s) of the shear links should not exceed sl,max = 0.75d(1 + cotα)
where:
Asw = area of shear reinforcement in length s (one link with 2 legs = 2 x leg area)
s = spacing of links measured along the axis of the member
bw = breadth of the web of the menber
α = the angle between the link and the longitudinal axis of the member
fyk = characteristic yield strength of the reinforcement
b) Members With Shear Reinforcement
Clause 6.2.3 of BS EN 1992-1-1 uses a truss model to evaluate the shear resistance of concrete members with shear reinforcement. The concrete resists the compressive forces whilst the reinforcement resists the tensile forces.
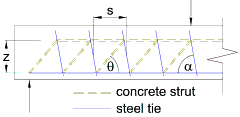
θ = the angle between the concrete compression strut and the longitudinal axis of the member. Values of θ between 45o and 21.8o (1 ≤ cotθ ≤ 2.5) may be used.
α = the angle between the link and the longitudinal axis of the member. Values of α between 45o and 90o may be used.
By considering vertical equilibrium on a section parallel to the line of the concrete strut it can be shown that the design shear force which can be resisted by the yielding shear reinforcement is:
VRd,s = Aswzfywd(cotθ+cotα)sinα/s .............. [Clause 6.2.3(4) equation (6.13)]
By considering vertical equilibrium on a section perpendicular to the line of the concrete strut it can be shown that the design shear force limited by compression in the concrete is:
VRd,max = αcwbwzν1fcd(cotθ+cotα)/(1+cot2θ) .............. [Clause 6.2.3(4) equation (6.14)]
where:
fywd = design yield strength of the shear reinforcement
αcw = 1.0 for non-prestressed structures
ν1 = 0.6(1-fck/250)(1-0.5cosα) .............. [UK NA to 1992-2 clause 6.2.3(103)]
Note: If stress of shear reinforcement is below 80% of fyk then ν1 = 0.54(1-0.5cosα)
c) Additional Longitudinal Reinforcement
Clause 6.2.3(107) of BS EN 1992-2 requires an additional tensile force ΔFtd = 0.5VEd(cotθ-cotα) to be resisted by the longitudinal reinforcement due to the force developed from the truss analogy.
The total force in the longitudinal steel due to bending and the truss force = MEd/z + ΔFtd. The total force should not be greater than MEd,max/z where MEd,max is the maximum moment along the beam.
Contact David Childs