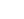Influence Line Tutorial for HA UDL and HB Loading Bending Effects
Example: Three span deck with continuity over pier supports.

Step1: Determine the position of the point of maximum bending moment in each element for a single point load.

Point A − maximum sagging moment in span 1
Point B − maximum hogging moment over pier 1
Point C − maximum sagging moment in span 2
Note: as end spans are equal then critical points over pier 2 and in span 3 can be
obtained from point A and B by symmetry.
Step 2: Determine influence line diagram for point A:
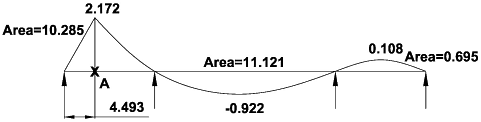
Step 3: Determine influence line diagram for point B:
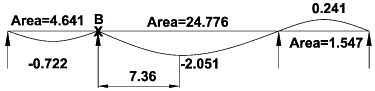
Step 4: Determine influence line diagram for point C:
Step 5: Determine loading for critical cases:
Point A
The maximum sagging moment is achieved by loading spans 1 and 3, however we also
need to check HA UDL for loading in span 1 only.
HA Span 1 only: loaded length = 10m hence udl = 71.8 kN/m (BD37-table 13)
HA Span 1 and 3: loaded length = 20m hence udl = 45.1 kN/m (BD37-table 13)
KEL: = 120 kN (BD37- Clause 6.2.2)
HB loading will produce worst sagging moment with an axle at the maximum ordinate (2.15). Any one of the 4 axles can be located at this position; the vehicle is however positioned with the other 3 axles to achieve the maximum total ordinates:
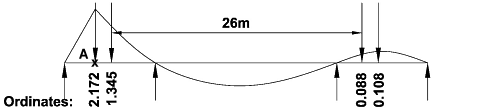
Note: The HB vehicle has a range of spacings between the centre axles, in this case
the 26m spacing gives the worst effect.
Point B
The maximum hogging moment is achieved by loading spans 1 and 2, however we also
need to check HA UDL for loading in span 2 only.
HA Span 2 only: loaded length = 20m hence udl = 45.1 kN/m (BD37-table 13)
HA Span 1 and 2: loaded length = 30m hence udl = 34.4 kN/m (BD37-table 13)
KEL: = 120 kN (BD37- Clause 6.2.2)
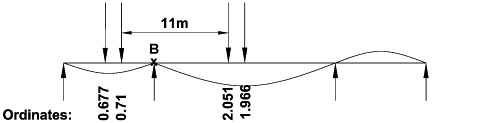
Usually HB loading will produce the worst hogging moment with an axle at the maximum ordinate
(2.051). Any one of the 4 axles can be located at this position; the vehicle is however
positioned with the other 3 axles to achieve the maximum total ordinates.
In the case below the sum of the ordinates is 0.677 + 0.71 + 2.051 + 1.966 = 5.404
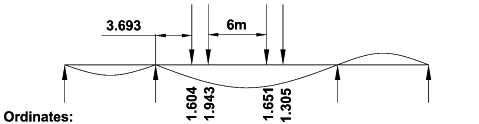
Other cofigurations of HB loading need be checked, and in this case the 6m vehicle will produce a greater value with the vehicle in the position shown below. The sum of the ordinates for this configuration = 1.604 + 1.943 + 1.651 + 1.305 = 6.503
Point C
The maximum sagging moment is achieved by loading span 2 only.
HA Span 2 only: loaded length = 20m hence udl = 45.1 kN/m (BD37-table 13)
KEL: = 120 kN (BD37- Clause 6.2.2)
HB loading will produce worst sagging moment with an axle at the maximum ordinate (3.125). Any one of the 4 axles can be located at this position; the vehicle is however positioned with the other 3 axles to achieve the maximum total ordinates:
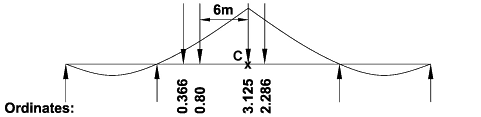
Note: The HB vehicle has a range of spacings between the centre axles, in this case
the 6m spacing gives the worst effect.
Step 6: Determine load effects on deck.
The following assumptions will be made to demonstrate principles of influence lines:
• Assume loads applied to 1 notional lane width of deck (3.65m wide).
• Assume ultimate limit state hence use load factor γfL of 1.5 for HA loading and 1.3 for HB loading.
• Assume 30 units of HB.
Span 1
Maximum sagging moment due to HB loading:
M = 1.3 x 30 x 10 x (2.172 + 1.345 + 0.088 + 0.108) = 1448 kNm
Maximum sagging moment due to HA loading at point A:
Case 1 − Span1 loaded
M = 1.5 x (71.8 x 10.285 + 120 x 2.172) = 1499 kNm (HA critical)
Case 2 − Span1 and 3 loaded
M = 1.5 x [45.1 x (10.285 + 0.695) + 120 x 2.172] = 1134 kNm
Pier 1
Maximum hogging moment due to HA loading at point B:
Case 1 − Span 2 loaded
M = 1.5 x (45.1 x 24.776 +120 x 2.051) = 2045 kNm
Case 2 − Span1 and 2 loaded
M = 1.5 x [34.4 x (24.776 + 4.641) + 120 x 2.051] = 1887 kNm
Maximum hogging moment due to HB loading:
M = 1.3 x 30 x 10 x (1.604 + 1.943 + 1.651 + 1.305) = 2536 kNm (HB critical)
Span 2
Maximum sagging moment due to HA loading at point C:
Case 1 − Span 2 loaded
M = 1.5 x (45.1 x 25.25 + 120 x 3.125) = 2271 kNm
Maximum sagging moment due to HB loading:
M = 1.3 x 30 x 10 x (3.125 + 2.286 + 0.8 + 0.366) = 2565 kNm (HB critical)
Note: HB loading is shown to be critical for two of the cases, however if the loads are distributed
using a computer analysis, such as a grillage analysis, then the HB moments will be
reduced considerably.
A spreadsheet (InfLine.zip) is availble to download which will provide the influence line diagram, areas and ordinates required to determine critical moments as detailed above.