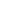Load Models 1 & 3 Example
BS EN 1991-2:2003 & UK National Annex
Clause 4.3.2 Load Model 1 & Clause 4.3.4 Load Model 3
Problem:
How do you work out the mid span bending moment by hand for a bridge deck under LM1 and LM3 loading for Groups gr1a and gr5 ?
Example:
Carriageway = 6m wide
Deck span = 34m (centre to centre of bearings for a simply supported single span)
Design for a metre width of deck :
Cl 4.2.3. Table 4.1
Carriageway width 6m ≤ w
Number of notional lanes n1 = Int(w/3) = 2
Notional lane width = 3m
Cl 4.2.4.(4)
Analyse for worst condition under Lane 1
Clause 4.3.2 Load Model 1
Cl 4.3.2 Table 4.2.
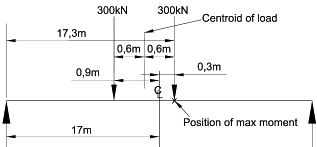
Each axle load of TS = αQ1Q1k = 1,0 x 300 = 300kN
The maximum moment for a simply supported span occurs under the axle
when the vehicle is positioned such that the mid span bisects the distance
between the centroid of the load and the nearest axle.
With a 34m span and the axles spaced 1,2m apart, the leading axle
is placed at 0,3m from the mid span.
Cl 4.3.2 Table 4.2.
UDL system = αq1q1k = αq1 x 9 kN/m2
Cl NA2.12 Table NA.1
αq1 = 0,61
Hence UDL system = 0,61 x 9 = 5.5 kN/m2
Maximum mid span moment on 1m width of lane = 5,5 x 342/8 = 795 kNm
Although the positions of the maximum moment due to the TS system and the UDL system are in different positions it will give a suitable approximation for the total maximum bending moment to add the two effects together.
Total maximum moment due to LM1 = 1640 + 795 = 2435 kNm per metre width of lane.
(This is confirmed by a line beam analysis which gives a value of 2435,1 kNm at 17,205m from the left hand support.
Clause 4.3.4 Load Model 3 Loading
The UK National Annex Clause NA.2.16 and Figures NA.1 & NA.2 describe configurations for Special Vehicles for LM3 loading.
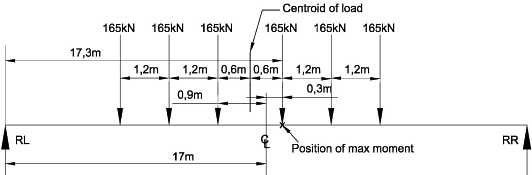
For this example we shall check for the load effects of the SV100 Vehicle.
All the axles will fit on the deck with any of the three options for the centre axle spacing (1.2, 5.0 or 9.0m). The worst mid span moment will be produced with the highest concentration of load at the centre of the deck therefore, by inspection, the SV100 vehicle with a centre axle spacing of 1.2m will produce the worst mid span moment.
The maximum moment for a simply supported span occurs under the inner axle
when the vehicle is positioned such that the mid span bisects the distance
between the centroid of the load and the nearest axle.
With a 34m span and the SV100 vehicle with equal axle loads, the inner axle
is placed at 0,3m from the mid span.
RR = 165(19,7+18,5+17,3+16,1+14,9+13,7)/34 = 486,3 kN
RL = 6x165-486.3 = 503,73kN
Moment at position of max moment = 486,3x16,7 - 165(1,2+2,4) = 7527kNm
UK NA Clause 2.16.3
A Dynamic Amplification Factor needs to be applied to the Basic Axle Loads.
From Table NA2 for a 165kN axle load the DAF = 1.12
Hence the moment on 1m width of the lane = 1.12 x 7527/3,0 = 2810 kNm
UK NA to BS EN 1991-2:2003 Table NA3 Groups of Traffic Loads
Group gr1a
Table NA 3 shows that the characteristic values of Load System LM1 is considered to act with 0,6 x characteristic value of the Footway Loading.
As we are considering a 1m width of deck then the footway load will not affect the magnitude of the load effects in Lane 1.
In practice there will be some effect from the footway loading on deck members under Lane 1 due to the transverse distribution through the deck slab. There will also be a reduction in the magnitude of the load effects from the LM1 System due to the same distribution effects.
There will be a net reduction in the load effects in Lane 1 if distribution effects are considered therefore the unit strip method will tend to overestimate the magnitude of the load effects.
Hence the Characteristic Value of the mid span moment for a 1m width of deck from Traffic Group gr1a = 2435 kNm.
Group gr5
Table NA 3 shows that the Frequent value of Load System LM1 is considered to act with the Characteristic values of Load System LM3.
NA to BS EN 1991-2:2003 Figure NA.4 shows how the TS and UDL systems of LM1 are to be arranged. The Lane numbers are interchangeable and the TS 300kN axles (for Lane 1) may be positioned adjacent to the SV vehicle instead of in the same lane.
As we are considering a unit strip then the 300kN axles will produce the worst effect in the same lane as the SV vehicle. However if transverse distribution is considered (as for a grillage analysis) then the 300kN axles may have a more onerous effect next to the SV vehicle in the adjacent lane.
RR due to UDL = 5,5(8,72/2 + 9,3 x 29,35)/34 = 50,3kN per metre width
RL due to UDL = 5,5(8,7 + 9,3) - 50,3 = 48,7kN per metre width
RR due to TS = 300(24,7 + 25,9)/34 = 446,5kN per 3 metre width
RL due to TS = 2 x 300 - 446,5 = 153,5kN per 3 metre width
Moment at mid span due to UDL = 50,3 x 17 - 5,5 x 9,3 x 12,35 = 223,4kNm per metre width
Moment at mid span due to TS = 153,5 x 17 = 2609,5kNm per 3 metre width
" " " "
" " " ≡ 2609,5/3 = 869,8kNm per metre width
Total mid span moment due to LM1 = 223,4 + 869,8 = 1093,2kNm per metre width of deck.
The Frequent value of LM1 is obtained by multiplying by ψ1
NA to BS EN 1990:2002+A1:2005 Table NA.A2.1 gives the frequent value factor ψ1 = 0,75 for both the TS and UDL components.
Hence the combined effect of LM1 and LM3 for the mid span moment for a 1m width of deck from Traffic Group gr5 = 2810 + 0,75 x 1093,2 = 3630 kNm.
Note: Although the position of the maximum moment for LM3 is not exactly at mid span the accuracy of the combined result with LM1 will be sufficient for a metre strip calculation.
Assuming that traffic loading is the leading action Qk,1 (which is usually the case) then:
SLS Characteristic combination moments are:
gr1a = 2435 kNm
gr5 moment = 3630 kNm
ULS moments are:
gr1a moment = 2435 x 1.35 = 3287 kNm
gr5 moment = 3630 x 1.35 = 4900 kNm
Hence the critical traffic loading for the mid span moment is from the Group gr5 combination.
Although it is not usual to use the unit strip method to design deck members it is a very useful exercise to obtain an approximate value of the load effects to enable a check to be carried out on the results of a grillage or finite element type distribution program.
Contact David Childs