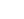BS EN 1992-2 DESIGN OF CONCRETE STRUCTURES
Click on the Clause No. for the commentary.
INDEX
| BS EN | CLAUSE No. | SUBJECT |
|---|---|---|
| 1992-1-1 Design of Concrete Structures |
3.1.4(6) | Differential Shrinkage |
| BS EN 1992-2 Design of Concrete Structures | |
|---|---|
| CLAUSE No. | SUBJECT |
| 3.1.4(6) | Differential Shrinkage |
Problem:
In determining the exposed perimeter 'u' for a pretensioned beam with insitu concrete deck slab:
1) Would the insitu deck soffit be considered as exposed with the presence of the permanent formwork?
2) Would the top of the insitu deck surface be considered as exposed with the presence of waterproofing?
Solution:
The response from the Eurocode Expert was:
“Most permanent formwork will prevent the majority of water loss from the insitu slab, but some drying shrinkage will occur before the waterproofing goes on from the upper surface.”
Having tried a few various solutions for when the waterproofing is applied and when the deck slab is cast, it is possible to present a Construction Programme which will, theoretically, produce negligible differential shrinkage between the insitu deck slab and precast beam.
This may sound desireable, but there could be disasterous consequencies if the beam has been manufactured and there is a delay in the Programme. It is reasonable to consider the Construction Programme as being similar to a design loading case and use the worse condition.
Below are examples of the results from different construction programmes.
Section Properties
Concrete Grades
Beam C40/50 fck = 40 N/mm2
Beam at transfer C32/40 fck = 32 N/mm2
Slab C32/40 fck = 32 N/mm2
BS EN 1992-1-1
Table 3.1
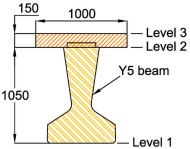
Consider modular ratio effect for different concrete strengths between beam and slab then:
Ecm,slab = 33.3GPa
Ecm,beam = 35.2GPa
Converting slab to beam units (fck = 40 N/mm2) then effective width of composite slab = 1000 × 33.3/35.2 = 946mm
Concrete Grade
C40/50 fck = 40 N/mm2
Note: The section has been simplified. The slab should be divided into 3 layers to account for the beam nib within the slab and the thickness of the permanent formwork.
Property
Beam Section
Composite Section
Area(mm2)
449.22×10 3
591.12×10 3
Centroid(mm)
456
625
2nd Moment of Area(mm4)
52.905×10 9
101.476×10 9
Modulus @ Level 1(mm3)
116.020×10 6
162.362×10 6
Modulus @ Level 2(mm3)
89.066×10 6
238.768×10 6
Modulus @ Level 3(mm3)
-
176.480×10 6
Differential Shrinkage Effects
BS EN 1992-1-1
cl.3.1.4(6)
The theoretical differential shrinkage between the beam and the deck slab can be calculated at every stage of construction and throughout the design life of the bridge.
Example of Staged Construction Calculation
(Not recommended unless the construction programme has been well defined.)
Assume the time scale for the stages of construction relative to the initial curing of the beam to be:
i) Stress transfer after initial set of concrete beam : t = 1 day
ii) Cast deck slab onto beams = 11/2 months : say t = 45 days
iii) Apply waterproofing to deck slab = 4 months : say t = 120 days
iv) Complete bridge and open to traffic = 6 months : say t = 180 days
Total shrinkage strain = εcs = εcd + εca .....................................................eqn.(3.8)
Where drying shrinkage strain εcd(t) = βds(t,ts) × kh × εcd,0 ........eqn.(3.9)
And autogenous shrinkage strain εca(t) = βas(t) × εca(∞) .................eqn.(3.11)
Shrinkage in Beam
Table 3.1
fcm = fck + 8 = 40 + 8 = 48N/mm2
Cross sectional area Ac = 449.22×10 3
Perimeter of beam in contact with atmosphere = u = 3100mm
Table 3.3
kh = 0.76 (by interpolation)
Eqn.3.10
βds(t,ts) = (t - ts) / [(t - ts) + 0.04 √(ho3)]
At begining of drying shrinkage: Age of concrete = ts = 1 day
βds(1,1) = 0 ......................(at transfer)
βds(1,45) = (45-1) / [(45-1) + 0.04 √(2903)] = 0.18 ......................(at casting deck)
βds(1,180) = (180-1) / [(180-1) + 0.04 √(2903)] = 0.48 .......................(at open for traffic)
βds(Long term) = 1.0
Annex B(B.11)
Basic drying shrinkage strain = 0.85[(220 + 110 ⋅ αds1) ⋅ exp(- αds2 ⋅ fcm / fcmo)] ⋅ 10-6 ⋅ βRH
Annex B(B.12)
βRH = 1.55[1 - (RH / RHo)3]
RH = 70%
RHo = 100% ∴ βRH = 1.02
It is probable that the beam will be constructed using rapid hardening cement ∴ assume cement Class R which gives:
αds1 = 6 αds2 = 0.11
fcm = 48N/mm2 fcmo = 10N/mm2
Hence Basic drying shrinkage strain = εcd,o = 450 με
Eqn 3.9
Drying shrinkage strain εcd(t) = βds(t,ts) × kh × εcd,0
At Stress Transfer
At Deck Cast
At Open to Traffic
Long Term
Units
t
1
45
180
∞
(days)
βds(t,ts)
0
0.18
0.48
1.0
εcd(t)
0
62
164
342
(με)
Eqn 3.12
Long term autogenous shrinkage strain = εca(∞) = 2.5(fck - 10)10-6 = (2.5 × 30)10-6 = 75 με
Eqn. 3.13
βas(t) = 1 - exp( - 0.2t0.5)
Eqn. 3.11
Autogenous shrinkage strain εca(t) = βas(t) × εca(∞)
At Stress Transfer
At Deck Cast
At Open to Traffic
Long Term
Units
t
1
45
180
∞
(days)
βas(t)
0.18
0.74
0.93
1.0
εca(t)
14
56
70
75
(με)
Eqn. 3.8
εcs = εcd + εca
Σ Shrinkage Strain
_________
14
_________
118
_________
234
_________
417
(με)
Shrinkage in Deck Slab
Following the same procedure for the beam the shrinkage in the deck slab can be estimated.
Table 3.1
fcm = fck + 8 = 32 + 8 = 40N/mm2
Cross sectional area Ac = 1000 × 150 = 150×10 3
Note:
Permanent formwork and waterproofing will reduce the perimeter of the deck which is exposed to drying.
An additional stage can be introduced for waterproofing between ‘casting the deck’ and ‘bridge open to traffic’. If the period between casting the deck and bridge opening is short then this stage could be omitted.
There is no moisture loss through the waterproofing so the top surface of the deck is assumed to be at the mid notional thickness of the member. Similarly with the permanent formwork, so for the notional size of the cross section:
Before waterproofing ho1 = 150 + 150 = 300mm
After waterproofing ho2 = 150 + 150 + 150 = 450mm
Table 3.3
Before waterproofing kh1 = 0.75
After waterproofing kh2 = 0.71
Assume an initial curing period ts of 3 days and Class N concrete.
Annex B(B.11)
Basic drying shrinkage strain = 0.85[(220 + 110 ⋅ αds1) ⋅ exp(- αds2 ⋅ fcm / fcmo)] ⋅ 10-6 ⋅ βRH
Annex B(B.12)
βRH = 1.02 (as before)
αds1 = 4 αds2 = 0.12
fcm = 40N/mm2 fcmo = 10N/mm2
Hence Basic drying shrinkage strain = εcd,o = 354 με
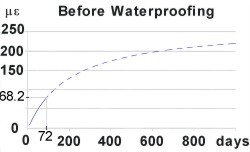
Initial period for drying shrinkage in deck slab is between deck casting and waterproofing (between day 45 and day 120 on the programme) so (t - ts) = (75 - 3) = 72 days.
βds(t,ts) = 72 / [72 + 0.04 √(3003)] = 0.257
εcd(t) = βds(t,ts) ⋅ kh1 ⋅ εcd,0 = 0.257 × 0.75 × 354 = 68.2 με
The next stage of the drying shrinkage, between waterproofing and open to traffic, has a reduced exposure surface. An estimated artificial start time for this period can be obtained which would give the same drying shrinkage (68.2 με) for the reduced exposure as was produced during the initial drying period.
(t - ts) ⋅ kh2 ⋅ εcd,0 = [(t - ts) + 0.04 √(ho23)] ⋅ εcd
(t - ts) × 0.71 × 354 = [(t - ts) + 0.04 × √(4503)] × 68.2
(t - ts) = 381.8 / 2.685 = 142 days
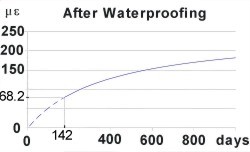
Artificial time when open to traffic = 142 + (180 - 120) = 202 days
So period for drying shrinkage in deck slab up to ‘open to traffic’ in terms of reduced exposure condition = (t - ts) = (202 - 3) = 199 days.
βds(t,ts) = 199 / [199 + 0.04 √(4503)] = 0.34
εcd(t) = βds(t,ts) ⋅ kh1 ⋅ εcd,0 = 0.34 × 0.71 × 354 = 85 με
Eqn 3.12
Long term autogenous shrinkage strain = εca(∞) = 2.5(fck - 10)10-6 = (2.5 × 22)10-6 = 55 με
At Waterproofing
At Open to Traffic
Long Term
Units
t
75
135
∞
(days)
t - ts
72
132
∞
(days)
Eqn. 3.13
βas(t)
0.82
0.90
1.0
Eqn. 3.10
βds(t,ts)
0.26
0.34
1.0
Eqn. 3.11
εca(t)
45
50
55
(με)
Eqn. 3.9
εcd(t)
68
85
251
(με)
Eqn. 3.8
εcs = εcd + εca
Σ Shrinkage Strain
_________
113
_________
135
_________
306
(με)
Differential shrinkage when bridge open to traffic = (135 - 0) - (234 - 118) = 19με
Long Term differential shrinkage = (306 - 0) - (417 - 118) = 7με
Note: If the deck is cast sooner than 45 days then the differential shrinkage is reduced. For example, if the deck is cast at 30 days then the long term differential shrinkage works out to be -10με which suggests the beam shrinks more than the insitu deck slab (a new phenomenon !).
( X close example )
However, at design stage, it could be a false economy to tie the contractor to a rigid construction programme in order to limit the differential shrinkage between the beam and the deck slab.
Any delays in pouring the deck slab, or applying the waterproofing would increase the differential shrinkage and this should be considered at design stage.
Assumptions
- Stress transfer after initial set of concrete beam : t = 1 day
- Cast deck slab onto beams = 6 months : say t = 180 days
(To allow for any unforseen dealays in casting the deck) - Complete bridge and open to traffic = 12 months : say t = 360 days
(Ignor effects of waterproofing as, in this case, it will reduce the differential shrinkage)
Total shrinkage strain = εcs = εcd + εca .....................................................eqn.(3.8)
Where drying shrinkage strain εcd(t) = βds(t,ts) × kh × εcd,0 ........eqn.(3.9)
And autogenous shrinkage strain εca(t) = βas(t) × εca(∞) .................eqn.(3.11)
Shrinkage in Beam
Table 3.1
fcm = fck + 8 = 40 + 8 = 48N/mm2
Cross sectional area Ac = 449.22×10 3
Perimeter of beam in contact with atmosphere = u = 3100mm
Table 3.3
kh = 0.76 (by interpolation)
Eqn.3.10
βds(t,ts) = (t - ts) / [(t - ts) + 0.04 √(ho3)]
At begining of drying shrinkage: Age of concrete = ts = 1 day
βds(1,1) = 0 ......................(at transfer)
βds(1,180) = (180-1) / [(180-1) + 0.04 √(2903)] = 0.48 ......................(at casting deck)
βds(1,360) = (360-1) / [(360-1) + 0.04 √(2903)] = 0.65 .......................(at open for traffic)
βds(Long term) = 1.0
Annex B(B.11)
Basic drying shrinkage strain = 0.85[(220 + 110 ⋅ αds1) ⋅ exp(- αds2 ⋅ fcm / fcmo)] ⋅ 10-6 ⋅ βRH
Annex B(B.12)
βRH = 1.55[1 - (RH / RHo)3]
RH = 70%
RHo = 100% ∴ βRH = 1.02
It is probable that the beam will be constructed using rapid hardening cement ∴ assume cement Class R which gives:
αds1 = 6 αds2 = 0.11
fcm = 48N/mm2 fcmo = 10N/mm2
Hence Basic drying shrinkage strain = εcd,o = 450 με
Eqn 3.9
Drying shrinkage strain εcd(t) = βds(t,ts) × kh × εcd,0
At Stress Transfer
At Deck Cast
At Open to Traffic
Long Term
Units
t
1
180
360
∞
(days)
βds(t,ts)
0
0.48
0.65
1.0
εcd(t)
0
164
222
342
(με)
Eqn 3.12
Long term autogenous shrinkage strain = εca(∞) = 2.5(fck - 10)10-6 = (2.5 × 30)10-6 = 75 με
Eqn. 3.13
βas(t) = 1 - exp( - 0.2t0.5)
Eqn. 3.11
Autogenous shrinkage strain εca(t) = βas(t) × εca(∞)
At Stress Transfer
At Deck Cast
At Open to Traffic
Long Term
Units
t
1
180
360
∞
(days)
βas(t)
0.18
0.93
0.98
1.0
εca(t)
14
70
74
75
(με)
Eqn. 3.8
εcs = εcd + εca
Σ Shrinkage Strain
_________
14
_________
234
_________
296
_________
417
(με)
Shrinkage in Deck Slab
Following the same procedure for the beam the shrinkage in the deck slab can be estimated.
Table 3.1
fcm = fck + 8 = 32 + 8 = 40N/mm2
Cross sectional area Ac = 1000 × 150 = 150×10 3
Note:
Permanent formwork and waterproofing will reduce the perimeter of the deck which is exposed to drying.
However, as the nature of formwork is not known and the timescale for waterproofing has not been defined, then, in this case, it is safer to assume these effects can be ignored.
So for the notional size of the cross section ho = 2 × 150×10 3 / 2000 = 150mm
Table 3.3
kh = 0.93
Assume an initial curing period ts of 3 days and Class N concrete.
Eqn.3.10
βds(t,ts) = (t - ts) / [(t - ts) + 0.04 √(ho3)]
At begining of drying shrinkage: Age of concrete = ts = 3 days
βds(3,3) = 0 ......................(at end of curing)
βds(3,180) = (180-3) / [(180-3) + 0.04 √(1503)] = 0.71 .......................(at open for traffic)
βds(Long term) = 1.0
Annex B(B.11)
Basic drying shrinkage strain = 0.85[(220 + 110 ⋅ αds1) ⋅ exp(- αds2 ⋅ fcm / fcmo)] ⋅ 10-6 ⋅ βRH
Annex B(B.12)
βRH = 1.02 (as before)
αds1 = 4 αds2 = 0.12
fcm = 40N/mm2 fcmo = 10N/mm2
Hence Basic drying shrinkage strain = εcd,o = 354 με
Eqn 3.9
Drying shrinkage strain εcd(t) = βds(t,ts) × kh × εcd,0
At Deck Cast
At Open to Traffic
Long Term
Units
t
3
180
∞
(days)
Eqn. 3.10
βds(t,ts)
0
0.71
1.0
Eqn. 3.9
εcd(t)
0
234
329
(με)
Eqn 3.12
Long term autogenous shrinkage strain = εca(∞) = 2.5(fck - 10)10-6 = (2.5 × 22)10-6 = 55 με
Eqn. 3.13
βas(t) = 1 - exp( - 0.2t0.5)
Eqn. 3.11
Autogenous shrinkage strain εca(t) = βas(t) × εca(∞)
At Deck Cast
At Open to Traffic
Long Term
Units
t
3
180
∞
(days)
Eqn. 3.13
βas(t)
0.29
0.93
1.0
Eqn. 3.11
εca(t)
16
51
55
(με)
Eqn. 3.8
εcs = εcd + εca
Σ Shrinkage Strain
_________
16
_________
285
_________
384
(με)
Differential shrinkage when bridge open to traffic = (285 - 16) - (296 - 234) = 207με
Long Term differential shrinkage = (384 - 16) - (417 - 234) = 185με
(It is worth noting that a value of 200με, for the Differential Shrinkage Strain between the slab and beam, was assumed in the BS 5400 design).