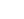BD 31/01 Design of Buried Concrete Box Structures
Click on the Clause No. for the commentary.
INDEX
Clause 3.2.8
Problem:
What are the maximum and minimum effective temperatures for cover depths between 0.2m and 0.6m as they are not included in BD 37?
Solution:
BD 31 makes no distinction for temperatures on structures with cover depths between 0.2m and 0.6m. BD 91 clauses 3.3.4 to 3.3.6 make allowances for different fill depths over the structure which resolves the anomoly in BD 31.
Background information to the development of the National Annex to BS EN 1991-1-5: 2003 says that there is very limited research on the temperature in buried structures, and no evidence to justify the difference in approach to the treatment of thermal actions in BD31/01 and BD91/04.
Both Standards were reviewed in drafting the NA and the approach given in BD91/04 was adopted as there was little physical justification for the way BD31/01 treated temperature differences.
It would therefore be reasonable to adopt the BD 91 solution if the values obtained from BD 31 were too onerous.
Back to Workshop | Back to Index
Clause 4.1.2
Problem:
How to determine the torsional moment from the earth pressues due to skew.
Solution:
This is not a definitive solution, but has been proposed to promote discussion.
Example:
2.5 × 2.0m box with 0.3m thick concrete walls
Joints at 10m centres with 45° skew
0.2m road construction (γ = 24kN/m3)
0.8m fill (γ = 20kN/m3)
2.0m backfill (γ = 19kN/m3)
Design angle of base friction = 20°
Use BD 31/01 Diagram A/6a loading combination.
cl.4.1.2(d)(ii)
(Excluding live load surcharge)
Minimum superimposed dead load on roof:
Surfacing = 0.2 × 24 = 4.8kN/m2
Fill = 0.8 × 20 = 16kN/m2
Total = 20.8kN/m2
(γfL = γf3 = 1.0)
Self weight of box = [(2.5 × 2.0) - (1.9 × 1.4)] × 25 = 58.5kN/m
Active earth pressures on box (γfL = 1.5 γf3 = 1.1):
Pressure at base due to backfill = 1.1 × 1.5 × K × 19 × 2.0 = 62.7K kN/m2
Active Force F1 = 62.7K × 2.0 / 2 = 62.7K kN/m
Pressure at base due to surcharge = 1.1 × 1.5 × K × 20.8 = 34.3K kN/m2
Active Force F2 = 34.3K × 2.0 = 68.6K kN/m
cl.3.2.1(a)(ii)
Fill depth > 0.6m hence use 30 units of HB
Wheel load = 30 × 10 / 4 = 75kN
BD37/01 cl.6.10.2
Traction Force = 25% × 30 × 10 × 4 = 300kN
BD31/01 cl.3.2.7(e)
Kt = (LL - H)/(LL - 0.6) = (2.5 - 1.0)/(2.5 - 0.6) = 0.789
(γfL = 1.1 γf3 = 1.1)
Traction Force applied to the roof = 1.1 × 1.1 × 0.789 × 300 = 286.4kN
BD31/01 cl.3.2.7(g)
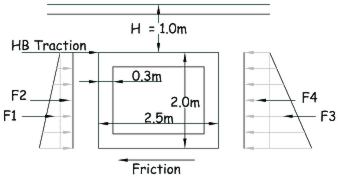
For plan rotation effects distribute the traction force along Lj
Assume a worst case that the full traction force is applied to the roof but only the wheels over the structure are contributing to the frictional resistance.
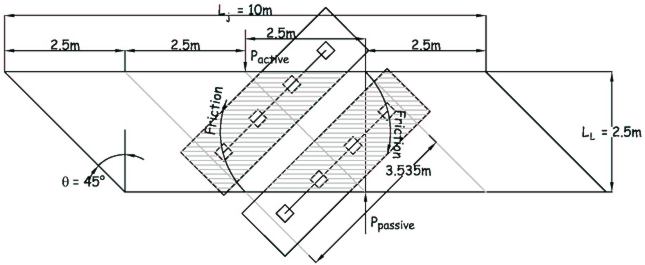
From Diagram A/6a for active pressures K = 0.33
Total active force Pactive = 286.4 + F1 + F2 = 286.4 + (62.7 + 68.6) × 0.33 × 10.0 = 719.7kN
Offset between Pactive and Ppassive = 2.5m hence applied torque = 719.7 × 2.5 = 1799kNm
Friction on the base of the structure will resist the torque created by the offset between the Passive and Active forces represented in the sketch by Ppassive and Pactive
Total vertical force on base (γfL = γf3 = 1.0) = (20.8 × 2.5 + 58.5) × 10 + 6 × 75 = 1555kN
Assume rotation at mid length of structure then frictional torque resistance is provided by two halves of structure at 5.0 / √2m
Hence frictional torque = 0.5 × 1555 × tan20° × 3.535 = 1000kNm
Net torque to be resisted by passive pressure = 1799 - 1000 = 799kNm
cl.4.1.2(d)(ii)
LLtanθ = 2.5 × tan45° = 2.5m ≥ Lj/6 = 10/6 = 1.67 hence increase horizontal earth pressure to resist unbalanced torque.
Passive earth pressures on box (γfL = γf3 = 1.0):
Pressure at base due to backfill = K × 19 × 2.0 = 38K kN/m2
Passive Force F3 = 38K × 2.0 / 2 = 38K kN/m
Pressure at base due to surcharge = K × 20.8 = 20.8K kN/m2
Passive Force F4 = 20.8K × 2.0 = 41.6K kN/m
F3 + F4 = 79.6K kN/m
Using the pressure diagram for an eccentrically loaded slab then the maximum pressure = P/A + M/Z
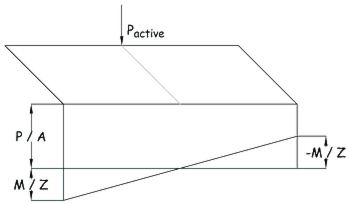
P/A = 719.7 / 2.0 / 10.0 = 36kN/m2
M/Z = 799 / 2.0 / 10.02 = 4kN/m2
Maximum Pressure = 36 + 4 = 40kN/m2
Maximum Force = 40 × 2.0 = 80kN/m
Hence maximum K required = 80 / 79.6 = 1.01 < 0.5Kp = 1.5 ∴ OK
Back to Workshop | Back to Index
Clause 4.3.5
Problem:
How to determine the ultimate moment of resistance of the corner reinforcement for opening moments.
Solution:
A method for the design is given in Appendix D.
Example:
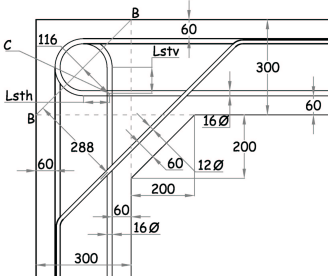
Type 2 corner detail shown. Refer to Figure D/2 of BD 31/01 for Notations.
Assume:
fcu = 40 N/mm2
Main bar reinforcement = B16@125 c/c (As = 1608mm2/m)
BD 31/01 cl. D.3
Fillet bar reinforcement = B12@125 c/c (As = 905mm2/m > 1608/2 = 804mm2/m)
Cover to reinforcement = 60mm throughout.
then:
BS 5400 Pt 4 cl. 5.8.6.9
Maximum allowable bearing stress = 1.5fcu/(1+2Φ/ab) = 1.5×40/(1+2×16/125) = 47.8 N/mm2
Allowable tensile force due to ultimate loads in a bend in a bar = Fbt = rΦ×Bearing stress
r = 300/2-(60+16) = 74
Fbt = 74×16×47.8×10-3 = 56.6kN
Table 14
For type 2 deformed bars in tension allowable bond stress fb = 4.0 N/mm2
BD 31/01 cl. D.4
Consider maximum allowable tension in main bars at C
Lst = 300/2 - 60 - 16/2 = 82mm
Maximum allowable tension = fbπΦLst + Fbt = 4×π×16×82×10-3+56.6 = 73.1 kN
Stress due to this force = 73.1×103/82π = 363.6N/mm2
BS 5400 Pt 4 cl. 4.3.3.3
γms = 1.15
fy/γms = 500/1.15 = 434.8N/mm2 > 363.6 hence use 363.6N/mm2
Hence maximum allowable tensile forces Fsh and Fsv = 363.6×82×π×10-3 = 73.1 kN
BD 31/01 Fig D/2
df = 300/√2 + 200/√2 - 60 - 6 = 288mm
BS 5400 Pt 4 cl. 5.3.2.3
Laf = [1-(1.1fyAs)/(fcubd)]d = [1-(1.1×500×905)/(40×1000×288)]d = 0.957d > 0.95d
Hence Laf = 0.95d = 0.95×288 = 274mm
La = [300 -2(60+8)]/√2 - (288-274) = 116 - 14 = 102mm
BD 31/01 Fig D/2
Design strength of fillet bars = Fsf = fyAs/γm = 500×905×10-3/1.15 = 393.5kN
Mr = FsfLaf + (Fsh+Fsv)La/√2 = 393.5×274×10-3 + 2×73.1×102×10-3/√2 = 118kNm