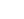BD 56/10 Assessment of Steel Highway Bridge Structures
Click on the Clause No. for the commentary.
INDEX
| CLAUSE No. | SUBJECT |
|---|---|
| 9.6.4.1.3 | Live Load rating of a plate girder with U-frame restraint. |
Clause 9.6.4.1.3 Beams with U-frame restraints
Problem:
Based on the moment capacity, what is the live load rating of a riveted plate girder with U-frame restraint. ?
Example:
Carriageway = 6m wide
Verges = 1m and 0.64m wide
Construction Depth at Verges = 0.9m
Construction Depth at Carriageway = 0.8m
Main Girders - Mid Span Section:
Top and Bottom Flanges: 508 × 38mm plate
Web: 2286 × 9 mm plate
Main Girders - End Section:
Top and Bottom Flanges: 508 × 25mm plate
Web: 2286 × 11 mm plate
Flange Angles: 102 × 102 × 14mm
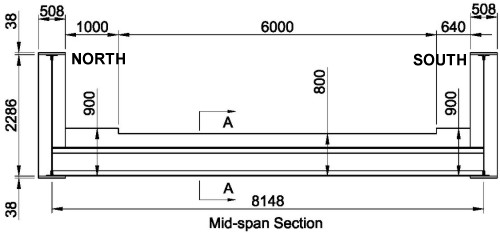
Cross Girders :
Top Flange: 254 × 19mm plate
Flange: 356 × 12 mm plate
Web: 508 × 9mm plate
Flange Angles: 89 × 89 × 12mm
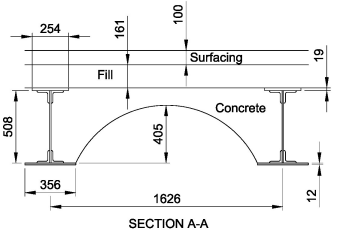
Web stiffeners are positioned at each cross girder and consist of 12mm gusset plates with 89 × 89 × 12mm angles alternating with 127 × 76 × 11mm T's.
The main girders are bedded on 508 × 1118 × 12mm thick plates on large masonry pad stones.
Records show that the bridge was built in 1925 so, from BD 21/01 Clause 4.3, the matal shall be assumed to be of steel with a characteristic yield strength of 230 N/mm2.
Dead Load :
Cl. 4.1. Table 4.1.
Main Girder self weight :
Cross sectional area of plates and angles (from spreadsheet ″Sectionprop5610.xls″)
= 69822mm2/m
Allowing 10% for web stiffeners and gusset plates then:
Self weight = 69822 × 1.1 × 7850 × 9.81 × 10-9 = 5.91kN/m
Cross Girder self weight :
Cross sectional area of plates and angles (from spreadsheet ″Sectionprop5610.xls″)
= 21638mm2/m
Allowing 10% for fittings then:
Self weight = 21638 × 1.1 × 7850 × 9.81 × 10-9 = 1.83kN/m
Infill concrete :
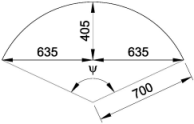
Radius of jack arch = (6352 + 4052)/(2 × 405) = 700mm
ψ = 2Sin-1(635/700) = 130°
Area of arch = 0.5 × r2( ψ° / 180° - Sinψ°) = 0.368m2
ψ° / 180° - Sinψ°) = 0.368m2
Area of infill concrete = (1.626 - 0.009)(0.508 + 0.019) - 0.368 = 0.484m2
Weight of infill concrete = 0.484 × 2300 × 9.81 × 10-3 = 10.92kN/m
Depth of Road construction above jack arch = (800 - 12 - 508 - 19) = say 260mm
From Note to Table 3.1: surfacing depth = 100mm
Therefore fill depth = 260 - 100 = 160mm
Weight of fill = 0.16 × 2200(miscellaneous fill) × 9.81 × 10-3 = 3.45kN/m2
Weight of surfacing = 0.1 × 2300(Asphalt) × 9.81 × 10-3 = 2.26 kN/m2
Weight of verges (above fill) = 0.2 × 2300(Asphalt) × 9.81 × 10-3 = 4.51 kN/m2
Cl. 3.7. Table 3.1
Applying Partial Load Factors γfL we get:
Main girder self weight = 1.05 × 5.91 = 6.21 kN/m
Cross girder self weight = 1.05 × 1.83 = 1.92 kN/m
Concrete = 1.15 × 10.92 = 12.56 kN/m
Fill = 1.2 × 3.45 = 4.14 kN/m2
Surfacing = 1.75 × 2.26 = 3.96 kN/m2
Verges = 1.2 × 4.51 = 5.41 kN/m2
The load path for distributed loads on the deck to the main girders is via the cross girders. These loads could be represented more accurately by point load reactions at the end of the cross girders, however it will be sufficiently accurate to represent them as uniformly distributed loads to simplify the calculation.
Reactions from the loads applied as a unifomly distributed load to each main girder:
Self Weight = 6.21 kN/m
Cross Girders = 1.92 × 8.148 / (2 × 1.626) = 4.81 kN/m
Concrete = 12.56 × 8.148 / (2 × 1.626) = 31.47 kN/m
Fill = 4.14 × 8.148 / 2 = 16.85 kN/m
Sub-Total = 59.34 kN/m
Uniformly distributed reactions from the surfacing and verge loads to each main girder:
North Main Girder:
Surfacing = 3.96 × 6.0 × 3.894 / 8.148 = 11.36 kN/m
North Verge = 5.41 × 1.0 × 7.394 / 8.148 = 4.91 kN/m
South Verge = 5.41 × 0.64 × 0.574 / 8.148 = 0.24 kN/m
Sub-Total = 16.51 kN/m
South Main Girder:
Surfacing = 3.96 × 6.0 × 4.254 / 8.148 = 12.40 kN/m
North Verge = 5.41 × 1.0 × 0.754 / 8.148 = 0.50 kN/m
South Verge = 5.41 × 0.64 × 7.574 / 8.148 = 3.22 kN/m
Sub-Total = 16.12 kN/m
Total Assessment Dead Load on each girder:
North Main Girder = 59.34 + 16.51 = 75.85 kN/m
South Main Girder = 59.34 + 16.12 = 75.46 kN/m
Cl. 16A Fig. 16.1A
The Effective Span (not to be confused with the effective length
 e) of the main girders, for calculating the load effects only , may be determined by calculating the position of the 'Centroid of Pressure' in accordance with the pressure diagram shown in Fig. 16.1A of BD 56/10.
e) of the main girders, for calculating the load effects only , may be determined by calculating the position of the 'Centroid of Pressure' in accordance with the pressure diagram shown in Fig. 16.1A of BD 56/10.
Effective Span
(from spreadsheet ″EffectiveSpan.xls″)
= 17.725m
Maximum Mid span Dead Load Moment = 75.85 × 17.7252 / 8 = 2980 kNm
Restraint to the compression flange is only provided by U-frames.
Assume only web stiffeners with gusset plates, at 3.251m centres, are effective in restraining the compression flange.
Note: The 'T' stiffeners will act as web stiffeners but are unlikely to be strong enough to resist U-frame forces FR and Fc (calculated below).
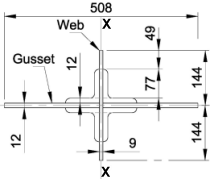
Effective width of web plate in stiffener = 16t = 16 × 9 = 144mm
I1 = IXX:
Gusset = 12 × 5083 / 12 = 131.097×106mm4
Angles = 2(12 × 1873 + 77 × 333) / 12 = 13.540×106mm4
Remaining web = 2 × 49 × 93 / 12 = 0.006×106mm4
I1 = (131.097 + 13.540 + 0.006)×106 = 144.643×106mm4
I2 = second moment of area of cross girder (from spreadsheet ″EffectiveSpan.xls″)
= Ixxnet = 1.056×109mm4
d1 = 38/2 + 2286 - (12 + 508 + 19) = 1766mm
d2 = 1766mm + depth to centroid of cross girder (ycnet)(from spreadsheet ″EffectiveSpan.xls″)
= 1766 + 251 = 2017mm
u = 0.5 for an outer girder
B = 8148mm
f = 0.5×10-10 for riveted cleat joint
E = 205000 N/mm2 (BD 21/01 Table 4.2)
δR = (d13/3EI1) + (uBd22/EI2) + fd22
δR = [17663 / (3 × 205000 × 144.643 × 106)] + [0.5 × 8148 × 20172 / (205000 × 1.056 × 109)] + 0.5 × 10-10 × 20172
δR = 6.192×10-5 + 7.656×10-5 + 20.341×10-5 = 34.189×10-5
Cl. 9.6.4.1.1.2
From Clause 9.6.4.1.3:
 R = 3251mm
R = 3251mm
δe = δe, max = δR = 34.189×10-5 (all U-frame stiffeners are the same)
a)
 e = k2k3k5
e = k2k3k5 1 but not less than k3
1 but not less than k3 R nor greater than L
R nor greater than L
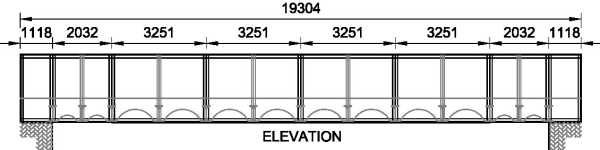
L = Distance between end U-frames = 19304 - (2 × 1118) = 17068mm
k2 = 1.0 (load applied via cross girder to bottom flange)
k3 = 1.0 (initial conservative assumption)
Ic = 38 × 5083 / 12 = 415 × 106mm4
 1 = (EIc
1 = (EIc RδR)0.25
RδR)0.25
 1 = (205000 × 415 × 106 × 3251 × 34.189×10-5)0.25 = 3118mm
1 = (205000 × 415 × 106 × 3251 × 34.189×10-5)0.25 = 3118mm
Χ =  13 / (√2EIcδe, max)
13 / (√2EIcδe, max)
Χ = 31183 / (√2 × 205000 × 415 × 106 × 34.189×10-5) = 0.737
k5 = 2.22 + 0.69 / (Χ + 0.5) = 2.22 + 0.69 / (0.737 + 0.5) = 2.78
 e = k2k3k5
e = k2k3k5 1
1
 e = 1.0 × 1.0 × 2.78 × 3118 = 8668mm
e = 1.0 × 1.0 × 2.78 × 3118 = 8668mm
Minimum  e = k3
e = k3 R = 1.0 × 3251mm < 8668mm ∴
R = 1.0 × 3251mm < 8668mm ∴  e = 8668mm (<17068)
e = 8668mm (<17068)
b)
 e =
e =  k2(EIc (δe1 + δe2) / L)1/2
k2(EIc (δe1 + δe2) / L)1/2
 e =
e =  × 1.0 × (205000 × 415 × 106 × 2 × 34.189×10-5 / 17725)1/2 = 5691mm
× 1.0 × (205000 × 415 × 106 × 2 × 34.189×10-5 / 17725)1/2 = 5691mm
 e = The greater of (a) and (b) = 8668mm
e = The greater of (a) and (b) = 8668mm
Cl. 9.7.1c)
Where intermediate restraints are not fully effective then, in accordance with Cl. 9.6.4.1.1.2 the definition for  w (the half-wavelength of buckling) is:
w (the half-wavelength of buckling) is:
L /  w = next integer below L /
w = next integer below L /  e but not less than 1.
e but not less than 1.
L = Distance between end U-frames = 19304 - (2 × 1118) = 17068mm
L / e = 17068 / 8668 = 1.97
e = 17068 / 8668 = 1.97
Hence L /  w = Integer(1.97) = 1
w = Integer(1.97) = 1
 w = L = 17068mm
w = L = 17068mm
Cl. 9.7.2
λLT =  e k4η
e k4η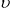 / ry
/ ry
Section properties (from spreadsheet ″EffectiveSpan.xls″)
Zpe (net) = 58.815×106 mm3
Ix (gross) = 74.270×109 mm4
Iy (gross) = 0.854×109 mm4
A (gross) = 69822 mm2
ry (gross) = 111 mm
h = 2286 + 38 = 2324 mm
k4 = [{4Z2pe(1-Iy/Ix)}/(A2h2)]1/4
k4 = [{4 × (58.815×106)2 × (1-0.854/74.270)} / (698222 × 23242)]1/4 = 0.85
Figure 10
A value of η < 1.0 can be obtained from Figure 10b) using Example 4 then:
MB / MA = 0
MA / MM = 0
From Figure 10b) η = 0.94
Ic = It ∴ i = Ic / (Ic + It) = 0.5 & ψi = 0.8(2i-1) = 0
λF = ( w / ry)( tf / D) = (17068 / 111)(38 / {2286 + 2×38}) = 2.474
w / ry)( tf / D) = (17068 / 111)(38 / {2286 + 2×38}) = 2.474
Table 9 Note 3
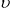 = [{4i(1-i)+0.05λF2+ ψi2}0.5+ψi]-0.5
= [{4i(1-i)+0.05λF2+ ψi2}0.5+ψi]-0.5
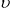 = [{4 × 0.5 (1 - 0.5) + 0.05 × 2.4742}0.5]-0.5 = 0.935
= [{4 × 0.5 (1 - 0.5) + 0.05 × 2.4742}0.5]-0.5 = 0.935
λLT = 8668 × 0.85 × 0.94 × 0.935 / 111 = 58.34
Cl. 9.8
The section is Non-Compact (from spreadsheet ″EffectiveSpan.xls″)
Hence Mult = the least of Zxc σyc or Zxt σyt (Web and flanges assumed to be of same steel grade ∴ Zxw σyw will not be critical)
Zxc (net) σyc = 59.922×106 × 230 × 10-6 = 13782 kNm
Zxt (net) σyt = 50.671×106 × 230 × 10-6 = 11654 kNm
∴ Mult = 11654 kNm
Mpe = Zpe (net) σyc = 58.815×106 × 230 × 10-6 = 13527 kNm
λLT[(σyc/355)(Mult/ Mpe)]0.5= 58.34[(230/355)(11654/13527)]0.5 = 43.59
Annex G G.8
β = λLT[(σyc/355)(Mult/ Mpe)]0.5 = 43.59
For Figure 11b): η = 0.0035(β - 30) = 0.0035(43.59 - 30) = 0.048
MR/Mult = 0.5[{1+(1+η)5700/β2}- ({1+(1+η)5700/β2}2-22800/β2)0.5]
MR/Mult = 0.5[{1+(1+0.048)(5700/43.592)}-({1+(1+0.048)(5700/43.592)}2 - 22800/43.592)0.5] = 0.935
MR = 0.933Mult = 0.935 × 11654 = 10896 kNm
9.9.1.2
MD = MR / γmγf3
4.3.3
γm = 1.05
γf3 = 1.1
MD = 10896 / (1.05 × 1.1) = 9434 kNm
Cl. 9.6.4.1.3
NOTE: The effective length  e has been calculated assuming that the U-frames comply with Clause 9.12.3, this will need to be confirmed later.
e has been calculated assuming that the U-frames comply with Clause 9.12.3, this will need to be confirmed later.
BD 21/01
The live load capacity of the main girder for bending at mid span = MD - Dead Load Moment
Live Load Capacity = 9434 - 2980 = 6454 kNm
Cl. 5.6
Notional Lane Width bL = 6.0 / 2 = 3.0 m (2 Notional Lanes)
Cl. 5.18
HA UDL and KEL:
W = 336(1/L)0.67 = 336(1/17.725)0.67 = 49 kN/m (of 3.65m lane width)
KEL = 120 kN
Cl. 5.22
Assume worst conditions for reduction factor:
High Traffic Flows and Poor Road Surfacing (Hp Traffic Condition)
From Figure 5.2 K Factor = 0.91 for 40 tonne level.
Cl. 5.23
Adjustment Factor (AF) = aL / 2.5 = 3.65 / 2.5 = 1.46
Cl. 5.25
Adjusted HA UDL and KEL for a 2.5 metre width of lane:
UDL W = 0.91 × 49 / 1.46 = 30.54 kN/m
KEL = 0.91 × 120 / 1.46 = 74.8 kN
Cl. 5.36(a)
Footway Live Load = 5.0 kN/m2
Cl. 5.37
Footway Live Load for elements supporting footways and carriageway = 0.8 × 5 = 4.0 kN/m2
Cl. 5.26
Adjusted HA UDL and KEL shall be applied to a 2.5m width within the lane for the worst effect:
Proportion the live load UDL's to each main girder as uniformly distributed reactions.
W1 = 4.0 × 1.0 = 4 kN/m
W2 = 30.54 kN/m
W3 = 4.0 × 0.64 = 2.56 kN/m
Cl. 3.7. Table 3.1
Applying Partial Load Factor γfL we get:
W1 = 1.5 × 4.0 = 6.0 kN/m
W2 = 1.5 × 30.54 = 45.81 kN/m
W3 = 1.5 × 2.56 = 3.84 kN/m
KEL = 1.5 × 74.8 = 112.2 kN
HA UDL and KEL positioned in the notional lane as shown above will produce the worst load effects in the South Girder.
Hence total live load UDL on South Girder:
W1 = 6.0 × 0.754 / 8.148 = 0.56 kN/m
North Lane W2 = 45.81 × 3.004 / 8.148 = 16.89 kN/m
South Lane W2 = 45.81 × 6.004 / 8.148 = 33.76 kN/m
W3 = 3.84 × 7.574 / 8.148 = 3.57 kN/m
Total Live Load UDL = 54.78 kN/m
Similarly total point load from KEL's on South Girder:
KEL = 112.2 × (3.004 + 6.004) / 8.148 = 124.04 kN
Maximum Mid span Live Load Moment:
M = 54.78 × 17.7252 / 8 + 124.04 × 17.725 / 4 = 2701 kNm
Live Load Capacity of Main Girder = 6454 kNm > 2701 kNm Hence mid span section OK for bending effects providing that the U-frames comply with Clause 9.12.3.
Note: If the moment capacity of the girder is insufficient for the dead + live load moment then a suitable K factor (Clause 5.25) will need to be applied to the live live moment. The live load moment of 2701 kNm already includes a K factor of 0.91 so the revised K factor needs to be applied to the full moment of 2701 / 0.91 = 2968 kNm.
Cl. 9.12.3.1
The cross members of each U frame may be assumed to be restrained by the concrete infill against movement in a direction normal to their compression flange.
Cl. 9.12.3.2
Strength: U-frames need to be checked for force FR (plus wind load if critical) calculated from Clause 9.12.2. Also a force Fc, from Clause 9.12.3.3, resulting from loads on the cross member, needs to be added to FR.
Cl. 9.12.2
FR = [ σfc / ( σci - σfc )] ×  w / (667δR) but not greater than
w / (667δR) but not greater than
[ σfc / ( σci - σfc )] × (n + 1)EIc / (16.7n  R2)
R2)
 w = 17068 mm
w = 17068 mm
δR = 34.189 × 10-5
Ic = 415 × 106 mm4
 R = 3251 mm
R = 3251 mm
Zpe net = 58.815 ×106 mm3
Zxc net = 59.922 ×106 mm3
λLT = 58.34
n = 5 (number of restraints in the half wavelength of buckling)
M = MDead + MLive = 2980 + 2701 = 5681 kNm
S = Zpe / Zxc = 58.815 / 59.922 = 0.982
σci =  2ES / λLT2 =
2ES / λLT2 =  2 × 205000 × 0.982 / 58.342 = 584 N/mm2
2 × 205000 × 0.982 / 58.342 = 584 N/mm2
σfc = M / Zxc = 5681 / 59.922 = 94.8 N/mm2
FR = [ σfc / ( σci - σfc )] ×  w / (667δR) = [ 94.8 / (584 - 94.8)] × 17068 × 10-3 / (667 × 34.189 × 10-5) = 14.5 kN
w / (667δR) = [ 94.8 / (584 - 94.8)] × 17068 × 10-3 / (667 × 34.189 × 10-5) = 14.5 kN
[ σfc / ( σci - σfc )] × (n + 1)EIc / (16.7n  R2) = [ 94.8 / (584 - 94.8)] × (5 + 1) × 205000 × 415 ×106 × 10-3 / (16.7 × 5 × 32512) = 112 kN
R2) = [ 94.8 / (584 - 94.8)] × (5 + 1) × 205000 × 415 ×106 × 10-3 / (16.7 × 5 × 32512) = 112 kN
∴ FR = 14.5 kN (< 112 kN)
Cl. 9.12.3.3
Fc = θd2 / [ 1.5δR + { R3 / (12EIc)} ]
R3 / (12EIc)} ]
θ is the difference in rotation between a cross member and the mean rotations of the cross members on either side of it.
As the dead load and HA UDL will have a similar effect on the rotaion for all cross members then θ for these loads = 0.
The KEL however will be applied to only one cross member so we need to determine θ for the KEL only (average θ of adjacent members = 0).
To calculate θ we can use the Moment Area theorem which states: The change in slope of the deflected shape of a beam between points A and B (A at end and B at mid-span) is equal to the area under the M/EI diagram between those two points.
The bending moment M at the centre of the cross girder with the two KEL in the lanes at W2 shown above:
Reactionnorth = 112.2(5.144 + 2.144) / 8.148 = 100.4 kN
Mid-span moment M = [100.4 × 4.074] - [112.2 × {1.25 + (4.074 - 3.004)}2 / (2.5 × 2)] = 288 kNm
It will be sufficiently accurate to assume a parabolic moment diagram as produced by a UDL.
θ = Area of M/EI diagram between mid-span and end = 2 × 4074 × 288 × 6 / (3 × 205000 × 1.056 × 109) = 3.613 × 10-3
d2 = 2017 mm
δR = 34.189 × 10-5
Ic = 415 × 106 mm4
 R = 3251 mm
R = 3251 mm
Fc = 3.613 × 10-3 × 2017 × 10-3 / [ 1.5 × 34.189 × 10-5 + { 32513 / (12 × 205000 × 415 × 106)} ] = 13.3 kN
Cl. 9.12.3.2
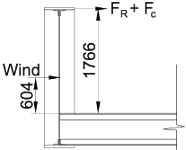
FR + Fc = 14.5 + 13.3 = 27.8 kN
Wind loading should be calculated in accordance with Clause 5.3 of BD 37/01 however a value of
6 kN/m2 may be used for general cases (see Clause 5.3.1 of BD 37/01).
Wind load on face of girder (per U-frame) = 6 × 2.362 × 3.251 = 46.1 kN
Note: Wind loading is Combination 2 loading which has a γfL = 1.25 for HA loading instead of 1.5 as used above, so FR and Fc may be reduced when combined with wind load. However continue with the calculated values for the example.
Moment in stiffener at top of cross girder = (27.8 × 1.766) + (46.1 × 0.604) = 77 kNm
Check bending capacity of stiffener:

IXX = 144.643×106mm4
IYY = 9 × 2883/12 + 24 × 1903/12 + 154 × 363/12 + 321 × 123/12 = 32.279 × 106 mm4
Area = 288 × 9 + 499 × 12 + 4(89 + 77) × 12 = 16548 mm2
Cl. 9.7.3.2
34tw /m × √(355/σyw) = [34 × 12 / 0.5] × [√(355/230)] = 1014 > 508 hence section is compact
Cl. 9.6.4 Table 8
 e = 1.4L = 1.4 × 1766 = 2472mm
e = 1.4L = 1.4 × 1766 = 2472mm
Cl. 9.7.2
λLT =  e k4η
e k4η / ry
/ ry
t f = 0 ∴ λF = 0 and 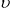 = 1.0
= 1.0
k4 = 1.0
Figure 10b)
MA = -M and MM = MB = 0:
MA / MM = -∞ and MB / MA = 0 then η = 0.76
ry = √(Iy/A) = √ ( 32.279 × 106 / 16548) = 44 mm
λLT = 2472 × 0.76 / 44 = 43
Cl. 9.8
 e /
e /  w = 1
w = 1
Mult = Mpe (section compact)
Zpe = 2 × [ (12 × 2542 / 2) + (24 × 93.52 / 2) + (154 × 16.52 / 2) + (98 × 16.52 / 2) = 1.053 × 106 mm3
Mpe = Zpeσyc = 1.053 × 106 × 230 × 10-6 = 242 kNm
λLT = 2472 × 0.76 / 44 = 43
λLT√[(σyc/355)(Mult/Mpe)] = 43 × √(230 / 355) = 35
Figure 11
MR / Mult = 0.94
Cl. 9.9.1.2
MD = MR / (γmγf3 = 0.94 × 242 / (1.05 × 1.1) = 197 kNm
197 > 77 ∴ the intermediate stiffeners are strong enough to restrain the main girder compression flange by U-frame action.
Cl. 9.12.5.1
The main girders also need to be restrained at their supports.
Note: Where the restraint provided is less than required to resist force FS then the slenderness parameter λLT must be modified as described in the addition to Clause 6.1 in BD 56/10.
Cl. 9.12.5.2.1
Restraining force FS = FS1 + FS2 + FS3 + FS4
Cl. 9.12.5.2.2
FS1 = 0.005 M / [df {1 - ( σfc / σci )2 } ]
M = 5681 kNm
df = 2286 + 25 = 2311 mm (25mm thick flanges at support)
σfc = 94.8 N/mm2
σci = 584 N/mm2
FS1 = 0.005 × 5681 × 103 / [2311 × {1 - ( 94.8 / 584 )2 }] = 12.7 kN
Cl. 9.12.5.2.3
FS2 = β( Δe1 + Δe2 ) σfc /({σci - σfc} Σδ )
β = 1.0
Δe1 = Δe2 = D / 200 = (2286 + 50) / 200 = 11.7 mm
Σδ = δt1 + δt2
δt = d13 / 3EI1 = 17663 / (3 × 205000 × 144.643×106) = 6.2 × 10-5
Σδ = 2 × 6.2 × 10-5 = 12.4 × 10-5
FS2 = 1.0 × 2 × 11.7 × 94.8 × 10-3/ ({584 - 94.8} × 12.4 × 10-5) = 36.6 kN
Cl. 9.12.5.2.4
FS3 = 0 as the load is applied directly through the bottom flange and bearing plate
Cl. 9.12.5.2.5
FS4 = 0 as there is no skew.
Cl. 9.12.5.2.6
FL = d2θ / [2.5δR + (δe / 2) + {  R3 / (3EIc)}]
R3 / (3EIc)}]
d2 = 2017 mm
θ = 3.613 × 10-3 radians
δR = δe = 34.189 × 10-5 mm
 R = 3251mm
R = 3251mm
Ic = 415 × 106 mm4
FL = 2017 × 3.613 × 10-3 × 10-3 / [(2.5 × 34.189 × 10-5) + (34.189 × 10-5 / 2) + {32513 / (3 × 205000 × 415 × 106)}] = 6.3 kN
FS + FL = 12.7 + 36.6 + 0 + 0 + 6.3 = 55.6 kN
Add in wind effects as for the internal U-frame, this is over-estimated as the end U-frames are closer together.
Moment in stiffener at top of cross girder = (55.6 × 1.766) + (46.1 × 0.604) = 126 kNm
Capacity of end stiffener is the same as the internal stiffener = 197 kNm > 126 ∴ end U-frame is adequate.
Having established that the U-frames are adequate then the main girder mid span section is able carry the full range of vehicles up to 40/44 tonnes gross weight as described in BD 21/01.
Note: All sections of the girder where plate sizes change (flange curtailment for example) or where corrosion has reduced the plate thickness, need to be checked for adequacy. Web plates also need to checked for shear effects; joints need to considered to ensure they can transfer loads to the relevant elements.
The live load capacity is determined by the weakest element in the bridge and a comprehensive check of every element needs to be caried out.