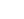Bending Capacity of Steel Beams to BS 5400 Pt.3
Beams in bending develop tension and compression in their flanges. The bending capacity of the beam is limited by how much force can be carried by each flange.
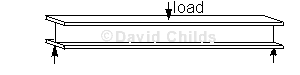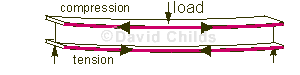
The tension flange acts like the string in an archer's bow and the maximum force that can be developed is limited only by the yield stress of the flange material.
The compression flange acts like a strut and is susceptible to buckling before yield stress can be developed. Unless the compression flange is fully restrained then the beam may fail by lateral torsional buckling.
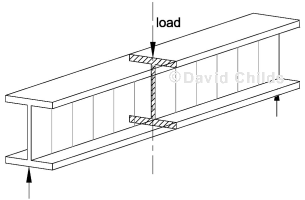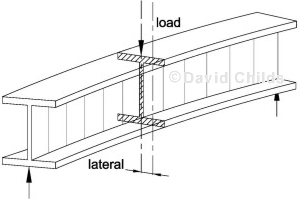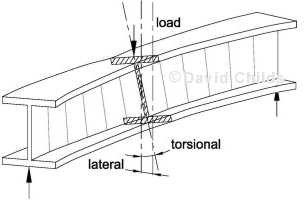
Lateral torsional buckling.
Clause 9.6.1 says if the second moment of area of a cross-section about the axis of bending (axis Y-Y in diagram below) is smaller than that about an axis perpendicular to it (axis X-X), the cross-section as a whole is stable against overall lateral torsional buckling and its effective length ( e) may be taken as zero.
e) may be taken as zero.
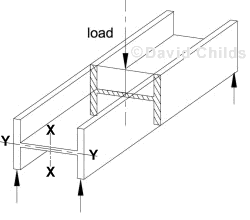
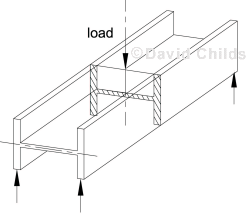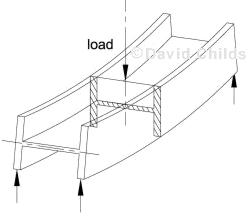
Clause 9.6.1 requires all beams to be restrained at their supports. The strength and stiffness of the restraints are checked using clause 9.12.5.
The restraint is required to hold the compression flange in place and is usually provided at the support by use of the bearing stiffeners and a suitable bearing and/or a bracing system.
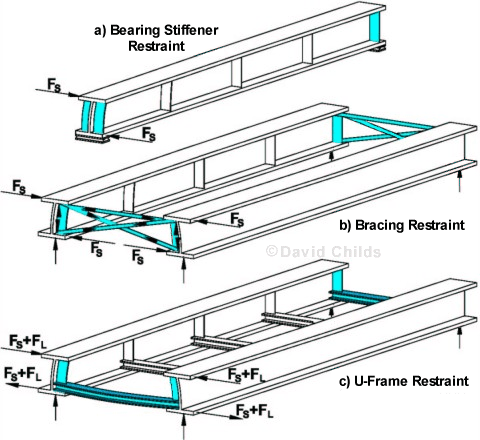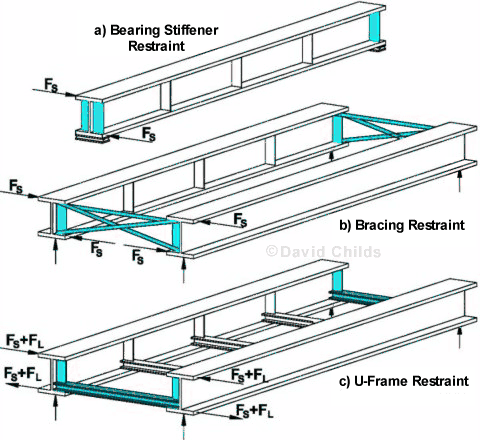
Clause 9.12.5 Restraint at support.
The restraining system is designed to resist the force FS (or FS + FL in the case of U-frames subjected to vertical loading on cross-beams) together with any coexistent forces such as wind or frictional forces.
The strength of the end restraint to resist FS is considered in isolation to the main beam(s) and any distribution effects along the length of the beam(s) are ignored.
Where only the bearing stiffener provides the torsional restraint {case (a)} then the stiffener has to be designed in accordance with Clause 9.14 as a load bearing support stiffener as well as satisfying the stiffness criteria of Clause 9.12.5.3. In cases (b) and (c) a bearing stiffener may be provided independently or incorporated into the restraining system.
The design procedure for checking a beam section is :
- From Clause 9.6
Determine the effective length ( e) based on the support condition of the compression flange.
The Code requires the compression flange to be supported laterally at the beams‘ supports in accordance with Clause 9.12.5.
This ensures that the compression flange can be assumed to have at least a pinned end support so the maximum
k1
(Clause 9.6.2) that may be assumed is 1.0 for non-cantilever beams.
If end diaphragms are provided to prevent the compression flange from rotating in plan then a smaller value of
k1can be used.
e) based on the support condition of the compression flange.
The Code requires the compression flange to be supported laterally at the beams‘ supports in accordance with Clause 9.12.5.
This ensures that the compression flange can be assumed to have at least a pinned end support so the maximum
k1
(Clause 9.6.2) that may be assumed is 1.0 for non-cantilever beams.
If end diaphragms are provided to prevent the compression flange from rotating in plan then a smaller value of
k1can be used.
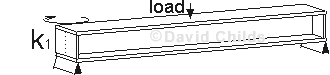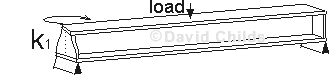
Rotational end restraint.
- Intermediate restraints to the compression flange can be provided to further reduce the effective length of the beam.
- These can take the form of:
- Plan bracing
- Torsional bracing
- U-Frames
- a) Plan Bracing
- This is only generally used as temporary bracing as it obstructs the deck construction on top of the beams. If the bracing is located on the underside of the compression flange then it is difficult to paint, for maintenance purposes, once the deck is in place.
- Clause 9.12.2a requires plan bracing to be able to resist force FR + any wind and other laterally applied forces.
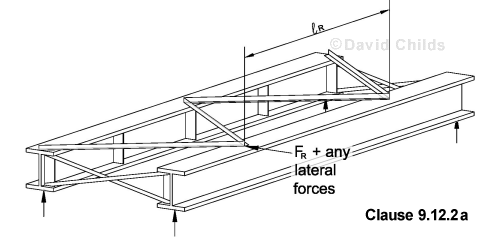
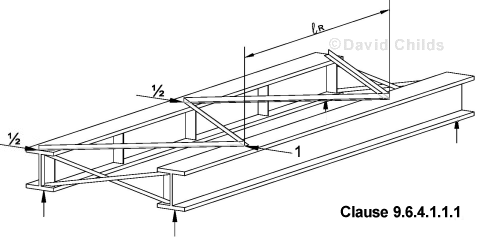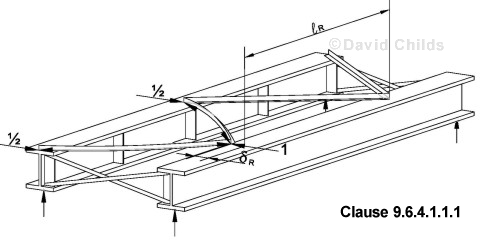
- If the plan bracing is fully effective {i.e. δR ≤
 R3 / (40 EIc) in accordance with Clause 9.6.4.1.1.1}
R3 / (40 EIc) in accordance with Clause 9.6.4.1.1.1}
then e =
e =  R
R
otherwise e has to be calculated using Clause 9.6.4.1.1.2.
e has to be calculated using Clause 9.6.4.1.1.2.
-
b) Torsional Bracing (Clause 9.12.2b)
Intermediate torsional bracing does not prevent the compression flange from moving laterally, but provides additional stiffness to resist the torsional displacement.
Some of the common types of bracing in use are shown below.
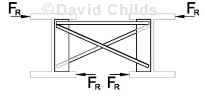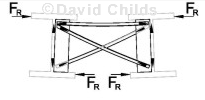
Cross Bracing

K Type Bracing
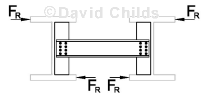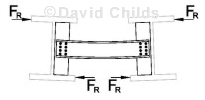
Channel Bracing
- Beams are often braced together in pairs before lifting on to their supports; this makes them stable during contruction.
If the deck slab is designed to restrain the compression flange, as in composite decks with shear connectors, then the intermediate bracing will be redundant when the deck is complete. The cost of removing the bracing and repairing the steelwork protection system is usually more expensive than the reclaim value of the steelwork and is therefore usually left in place. If the bracing is left in place then it will pick up load when the beams deflect under traffic loading and will therefore need to be checked for this loading condition.
Torsional restraints need to be checked in accordance with Clause 9.12.2b to be capable of resisting two transverse forces FR applied to the flanges.
The effective length e is then calculated using Clause 9.6.4.1.2.
e is then calculated using Clause 9.6.4.1.2.
-
c) U-Frames
U-frames are a characteristic of the 'Half Through' deck construction. The 'U' shape of the U-frame is formed by two vertical web stiffeners and the deck cross beam. The web stiffeners are attached to the compression flanges of the main edge girders and are able to resist the lateral buckling movement of the flange (see Clause 9.12.3.1).
The stiffness of the U-frame is evaluated by adding the stiffness of its components due to a unit force acting at the level of the compression flange and is determined using Clause 9.6.4.1.3:
δR = d13 / 3EI1 + uBd22 / EI2 + fd22
The deflection of the web stiffener acting as a cantilever (δi = d13 / 3EI1).
The effect from the cross beam bending (δii = uBd22 / EI2).
The flexibility of the joint between the cross beam and the vertical stiffeners (δiii = fd22).

δR = δi + δii + δiii
For end U-frames: δe = δi + δii + δiii
-
The effective length
 e is then calculated using Clause 9.6.4.1.1.2 with
e is then calculated using Clause 9.6.4.1.1.2 with  R equal to the intermediate U-frame spacing.
R equal to the intermediate U-frame spacing.
An example of determining the effective length for beams with U-frame restraint is given in the workshop section for BD 56/10 (The Assessment of Steel Highway Bridges).
- From Clause 9.7
Determine the slenderness (λLT) using the geometrical parameters of the beam. - From Clause 9.8
Determine the limiting moment of resistance (MR). - From Clause 9.9
Determine the bending capacity (MD) - From Clause 9.12.5
Determine the strength of the end restraint to provide adequate support to the compression flange.
Contact David Childs