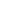Abutment Design Example to Eurocodes and UK National Annexes
Index
Design the fixed and free end cantilever abutments to the 20m span deck shown to carry Load Model 1 and vehicles SV80, SV100 and SV196 for Load Model 3. Analyse the abutments using a unit strip method. The bridge site is located south east of Oxford (to establish the range of shade air temperatures).
Vehicle collision on large abutments need not be considered as they are assumed to have sufficient mass to withstand the collision loads for global purposes.
The ground investigation report shows suitable founding strata about 9.5m below the proposed road level and 1.5m below existing ground level. Test results show the founding strata to be a well drained, cohesionless soil having an angle of shearing resistance (φ') = 34°, a critical state angle of shearing resistance (φ'cν) = 30° and a weight density = 19kN/m3.
Backfill material will be Class 6N with an angle of shearing resistance (φ'bf;k) = 35° and weight density (γbf;k) = 19kN/m3.
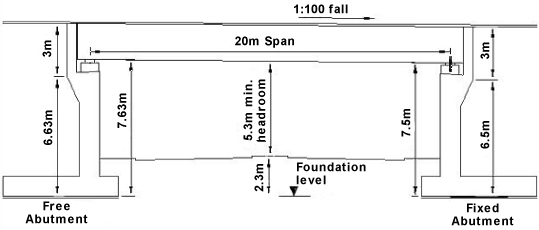
The proposed deck consists of 11No. Y4 prestressed concrete beams at 1m centres and concrete deck slab as shown.
EN 1997-1:2004 Clause 2.4.7.3.4.1(1)P - Use Design Approach 1 only for verification of resistance for structural and ground limit states in persistent
and transient situations (STR and GEO).
Consider Combination 1: A1 “+” M1 “+” R1 and Combination 2: A2 “+” M2 “+” R1
A grillage analysis gave the following characteristic reactions for the various load cases:
Critical Vertical Reaction Under One Beam
Characteristic Reaction
(kN)
ULS Reaction
(kN)
Concrete Deck
180
240
gr1a
290
430
gr5
270
400
gr6
210
300
Total Vertical Reaction on Each Abutment
Concrete Deck
1900
1.35 / 0.95
1.0 / 1.0
gr1a
1490
1.35 / 0
1.15 / 0
gr2
1120
1.35 / 0
1.15 / 0
gr5
1930
1.35 / 0
1.15 / 0
gr6
1470
1.35 / 0
1.15 / 0
Characteristic loading on 1m length of abutment:
Deck Dead Load = 1900 / 11.6 = 164kN/m
Maximum Surfacing = 1.55 × 320 / 11.6 = 43kN/m
Minimum Surfacing = 0.6 × 320 / 11.6 = 17kN/m
gr1a on Deck = 1490 / 11.6 = 128kN/m
gr2 on Deck = 1030 / 11.6 = 89kN/m
gr5 on Deck = 1930 / 11.6 = 166kN/m
gr6 on Deck = 1470 / 11.6 = 127kN/m
From UK NA to BS EN 1991-1-5:2003 Figures NA.1 and NA.2 the minimum and maximum shade air temperatures are -17 and +34°C respectively.
For bridge deck type 3 the corresponding minimum (Te,min) and maximum (Te,max) effective bridge temperatures are -11 and +36°C from BS EN 1991-1-5:2003 Figure 6.1.
Hence the temperature range = 11 + 36 = 47°C.
Form EN 1991-1-5 Table C.1 - Coefficient of thermal expansion for a concrete deck = 10 × 10-6 per °C.
However CIRIA Report C660 ("Early-age thermal crack control in concrete") suggests that a value of 10 × 10-6 per °C is unsuitable for some of the concrete aggregates used in the UK and suggest a value of 12 × 10-6 per °C should be used if the type of aggregate has not been specified.
Hence the range of movement at the free end of the 20m span deck = 47 × 12 × 10-6 × 20 × 103 = 11.3mm.
The design thermal movement in the deck will be ± [(11.3 / 2) γF] = ±[11.3 × 1.35 /2] = ± 8mm.
Option 1 - Elastomeric Bearing:
With a maximum ultimate reaction = 240 + 60 + 430 = 730kN then a suitable elastomeric bearing would be Ekspan's Elastomeric Pad:
Bearing EKR35:
- Maximum Load = 1053kN
- Shear Deflection = 13.3mm
- Shear Stiffness = 12.14kN/mm
- Bearing Thickness = 19mm
Note: the required shear deflection (8mm) should be limited to between 30% to 50% of the thickness of the bearing. The figure quoted in the catalogue for the maximum shear deflection is 70% of the thickness.
A tolerance is also required for setting the bearing if the ambient temperature is not at the mid range temperature.
The design shade air temperature range will be -17 to +34°C which would require the bearings to be installed at a shade air temperature of [(34+17)/2-17] = 9°C to achieve the ± 8mm movement.
If the bearings are set at a maximum shade air temperature (T0) of 16°C then, by proportion the deck will expand 8×(34-16)/[(34+17)/2] = 6mm and contract 8×(16+17)/[(34+17)/2] = 10mm.
Let us assume that this maximum shade air temperature of 16°C for fixing the bearings is specified for T0 in the Contract and design the abutments accordingly.
Horizontal load at bearing for 10mm contraction = 12.14 × 10 = 121kN.
This is an ultimate load hence the characteristic horizontal load = 121 / 1.35 = 90kN.
If a fixed abutment is used then the movement will take place at one end so:
Total horizontal load on each abutment = 11 × 90 = 990 kN ≡ 990 / 11.6 = 85kN/m.
If no fixed abutment is used then the movement will take place at both ends so:
Total horizontal load on each abutment = 85/2 = 43kN/m.
Option 2 - Sliding Bearing:
With a maximum ultimate reaction of 730kN and longitudinal movement of ± 8mm then a suitable bearing from the Ekspan EA Series would be /80/210/25/25:
- Maximum Load = 800kN
- Base Plate A dimension = 210mm
- Base Plate B dimension = 365mm
- Movement ± X = 12.5mm
Average characteristic permanent load reaction = (1900 + 320) / 11 = 2220 / 11 = 200kN
Contact pressure under base plate = 200000 / (210 × 365) = 3N/mm2
As the mating surface between the stainless steel and PTFE is smaller than the base plate then the pressure between the sliding faces will be in the order of 5N/mm2.
Ekspan recommend a coefficient of friction = 0.05, however use a coefficient of friction = 0.08 for long term exposure conditions.
Hence total horizontal load on each abutment when the deck expands or contracts = 2220 × 0.08 = 180kN ≡ 180 / 11.6 = 16kN/m.
Braking and Acceleration Force - BS EN 1991-2:2003 Clause 4.4.1:
(2) Characteristic Force for LM1 = 0.6αQ1(2Q1k)+0.1αq1qq1w1L = 0.6 × 1 (2 × 300) + 0.1 × 1 × 9 × 3 × 20 = 414kN
For global effects, braking force on 1m width of abutment = 414 / 11.6 = 36kN/m.
(NA. 2.18.1) Characteristic Force for LM3 (SV196) = Qlk,s = δw = 0.25 × (165kN × 9axles + 180kN × 2axles + 100kN × 1axle) = 486kN
For global effects, braking force on 1m width of abutment = 486 / 11.6 = 42kN/m.
When this load is applied on the deck it will act at bearing shelf level. If sliding bearings are used then friction forces at the free end should be considered as a relieving effect on longitudinal loads and therefore ignored.
Note: Braking forces should not be taken into account at the surfacing level of the carriageway over the backfill (See BS EN 1991-2:2003 Cl. 4.9.2)
Backfill
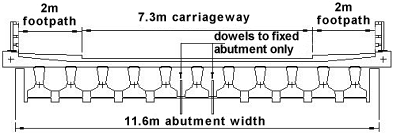
For Stability calculations use active earth pressures = Ka γbf;k h
For Design of Structural Members use at-rest earth pressures = K0 γbf;k h
SLS
Combination 1
Combination 2
φ'bf;d = tan-1[tan(φ'bf;k)/γM]
35.0°
35.0°
29.3°
Ka = (1-Sinφ'bf;d) / (1+Sinφ'bf;d)
0.271
0.271
0.343
K0 = 1-Sinφ'bf;d
0.426
0.426
0.511
Backfill density (γbf;d) = γbf;k γG;sup
19.0
25.65
19.0
Backfill density (γbf;d) = γbf;k γG;inf
19.0
18.1
19.0
Hap;d = γbf;dKaγSd;KZ2/2
2.575Z2kN/m
4.171Z2kN/m
3.91Z2kN/m
Surcharge - Use Horizontal Surcharge Model in PD 6694-1:2011 Figure 2:
Carriageway width = 7.3m ∴ there are 2 notional lanes of effective width Weff of 3m with 1.3m wide remaining area (see Table 4.1 of BS EN 1991-2:2003).
The vehicle model for loads on backfill behind abutments is positioned in each notional lane (see Clause NA.2.34.2 UK NA to BS EN 1991-2) ∴ the effective number of lanes (Nlane) in the surcharge model will be 2.
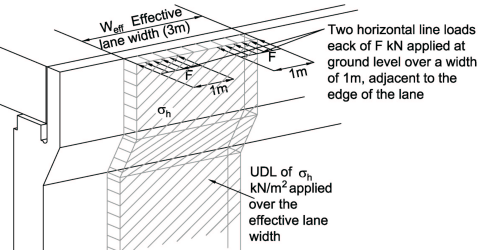
From PD 6694-1:2011 Table 7 :
Normal Traffic
Line Load kN/m = Hsc;F = F.Kd.Nlane/Wabut = 2×330Kd×2/11.6 = 113.79Kd
Note: Df is used for determining the distibution of the Line Load in the wall for a metre strip analysis, but is not included in the calculation when considering the overall stability of the wall.
UDL kN/m2 = σh;ave = σh.Wlane.Nlane/Wabut = 20×Kd×3×2/11.6 = 10.34Kd
SV/196 Traffic (SV/196 lane 1 + Frequent value of Normal Traffic in Lane 2)
Line Load kN/m (at ground level) = Hsc;F = F.Kd.(1 + ψ1)/Wabut = 2×330Kd×1.75/11.6 = 99.57Kd
UDL kN/m2 = σh;ave = (σh1+ψ1.σh2).Wlane/Wabut = (30+0.75×20)×Kd×3/11.6 = 11.64Kd
SLS
Combination 1
Combination 2
Partial Factor on Surcharge γQ
1.0
1.35
1.15
Assume Abutments are to be backfilled in accordance with the Highways Agency Manual of Contract Documents for Highway Works (MCHW), then compaction pressures due to construction vehicles are deemed to be coverered if the surcharge model in Figure 2 and Table 7 of PD 6694-1:2011 (as shown above) is employed (see PD 6694-1:2011 Clause 7.3.3).
Initial Sizing for Base Dimensions
There are a number of publications that will give guidance on base sizes for free standing cantilever walls, Reynolds's Reinforced Concrete Designer's Handbook being one such book.
Alternatively a simple spreadsheet will achieve a result by trial and error.
Load Combinations
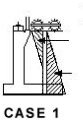
Backfill + Construction surcharge
(Not used - backfilled to MCHW - see PD 6694-1:2011 Clause 7.3.3)
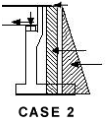
Backfill + Normal Traffic Surcharge + Deck Permanent load + Deck contraction/shrinkage
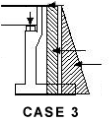
Backfill + Normal Traffic Surcharge + Deck Permanent load + gr1a on deck
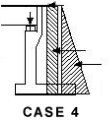
Backfill + SV/100 and SV/196 Surcharge + Deck Permanent load + gr1a (frequent value) on deck
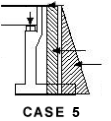
Backfill + Normal Traffic Surcharge (frequent value) + Deck Permanent load + gr5 on deck
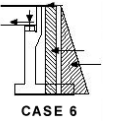
Backfill + Normal Traffic Surcharge (frequent value) + Deck Permanent load + gr2 (ψ1LM1 with braking on deck)
(Braking not applied to free abutment if sliding bearings are provided)
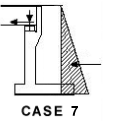
Backfill + Deck Permanent load + gr6 (LM3 with braking on deck)
(Braking not applied to free abutment if sliding bearings are provided)
Example of Stability Calculations:
CASE 6 - Fixed Abutment
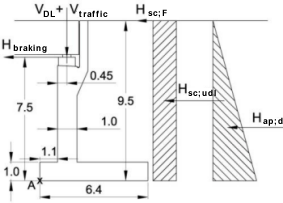
Density of reinforced concrete = 25kN/m3.
SLS (γG = γQ = γSd;K = 1.0)
Weight of wall stem = γG × twall × Zwall × γconc = 1.0 × 1.0 × 6.5 × 25 = 162.5kN/m
Weight of base = γG × Wbase × Zbase × γconc = 1.0 × 6.4 × 1.0 × 25 = 160kN/m
Weight of backfill = γG × Wheel × Zheel × γbf;d = 1.0 × 4.3 × 8.5 × 19 = 694.5kN/m
Backfill Force Hap;d = γG × γSd;K × Ka × γbf;d × Z2/2 = 1.0 × 1.0 × 0.271 × 19 × 9.52 / 2 = 232kN/m
Frequent value of Surcharge UDL Force Hsc;udl = ψ1 × γQ × σh;ave × Z = 0.75 × 1.0 × (10.34 × 0.271) × 9.5 = 20 kN/m
Frequent value of Surcharge Line Load Force Hsc;F = ψ1 × γQ × Hsc;F = 0.75 × 1.0 × (113.79 × 0.271) = 23 kN/m
Deck Maximum Permanent load (concrete + surfacingmax) = γG × VDL = 1.0 × (164 + 43) = 207kN/m
Deck Minimum Permanent load (concrete + surfacingmin) = γG × VDL = 1.0 × (164 + 17) = 181kN/m
Deck Vertical Traffic load (gr2) = γQ × Vtraffic = 1.0 × 89 = 89kN/m
Deck Horizontal Traffic load (gr2) = γQ × Hbraking = 1.0 × 36 = 36kN/m
Restoring Effects:
Minimum
V
Lever Arm
Moment About A
Stem
162.5
1.6
260
Base
160
3.2
512
Backfill
694.5
4.25
2952
Deck (VDLmin)
181
1.55
281
∑ =
1198
∑ =
4005
Maximum
V
Lever Arm
Moment About A
Stem
162.5
1.6
260
Base
160
3.2
512
Backfill
694.5
4.25
2952
Deck (VDLmax + Vtraffic)
296
1.55
459
∑ =
1313
∑ =
4183
Overturning Effects:
H
Lever Arm
Moment About A
Hap;d
232
3.167
735
Hsc;udl
20
4.75
95
Hsc;F
23
9.5
219
Hbraking
36
7.5
270
∑ =
311
∑ =
1319
For sliding effects:
φ'cν = 30°
Partial factor on γM on tan(φ'cν;k) = 1.0
Coefficient of friction = μd = tan(φ'cν;k) / γM = tan(30°)/1.0 = 0.58
Sliding resistance = μd∑Vmin = Rνx;d = 0.58 × 1198 = 695kN/m
Active Force = ∑H = 311kN/m < 695 ∴ OK
Bearing Pressure:
PD 6694-1 Cl. 5.2.2 requires no uplift at SLS
Check bearing pressure at toe and heel of base slab = (V / A) ± (V × e × y / I) where V × e is the moment about the centre of the base.
V = 1313kN/m
A = 6.4m2/m
I / y = 6.42 / 6 = 6.827m3/m
Nett moment = 4183 - 1319 = 2864kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (2864 / 1313) = 1.019m
Pressure under base = (1313 / 6.4) ± (1313 × 1.019 / 6.827)
Pressure under toe = 205 + 196 = 401kN/m2
Pressure under heel = 205 - 196 = 9kN/m2 > 0 ∴ OK (no uplift)
Also
BS EN 1997-1:2004, 2.4.8(4), allows the serviceability limit state for settlement to be verified by ensuring that a “sufficiently low fraction of the ground strength is mobilized”. This requirement can be deemed to be satisfied if the maximum pressure under a foundation at SLS does not exceed one third of the design resistance R/A' calculated in accordance with BS EN 1997-1:2004, Annex D, using characteristic values of φ', cu and γ' and representative values of horizontal and vertical actions.
From Annex D.4 for Drained Conditions:
R/A' = c'Ncbcscic + q'Nqbqsqiq + 0.5γ'B'Nγbγsγiγ
c' = 0
γ' = γ × γG;inf = 19 × 1.0 = 19kN/m3
q' = 1.5 × 19 = 28.5 kN/m2 (Foundation 1.5m below existing ground level)
Nq = eπtanφ'dtan2(45 + φ'd / 2)
φ'd = φ' = 34° (γM = 1.0)
Nq = eπtan34tan2(45 + 34 / 2) = 29.4
Nγ = 2(Nq - 1)tanφ'd = 2 × (29.4 - 1) × tan34 = 38.3
bq = bγ = 1.0 (α = 0)
B' = B - 2e = 6.4 - 2 × 1.019 = 4.362
sq = 1 + (B' / L')sinφ'd = 1 + (4.362 / 11.6) × sin34 = 1.21
sγ = 1 - 0.3(B' / L') = 1 - 0.3(4.362 / 11.6) = 0.89
m = (2 + B' / L') / (1 + B' / L') = (2 + 4.362 / 11.6) / (1 + 4.362 / 11.6) = 1.73
iq = [1 - H / (V + A'c'dcotφ'd)]m = [1 - 311 / 1313]1.73 = 0.63
iγ = [1 - H / (V + A'c'dcotφ'd)]m+1 = [1 - 311 / 1313]2.73 = 0.48
R/A' = 0 + (28.5 × 29.4 × 1.0 × 1.21 × 0.63) + (0.5 × 19 × 4.362 × 38.3 × 1.0 × 0.89 × 0.48 = 639 + 678 = 1317 kN/m2
1/3(R/A') = 1317 / 3 = 439 kN/m2 > 401 kN/m2 ∴ settlement check OK.
ULS Check Combination 1 and Combination 2.
γG;sup
γG;inf
γQ
γSd;K
Combination 1
Combination 1 Surfacing
1.35
1.2
0.95
0.95
1.35
1.2
Combination 2
1.00
1.00
1.15
1.2
Comb.1
Comb.2
Min. weight of wall stem = γG;inf × twall × Zwall × γconc
154
162.5
Max. weight of wall stem = γG;sup × twall × Zwall × γconc
219
162.5
Min. weight of base = γG;inf × Wbase × Zbase × γconc
152
160
Max. weight of base = γG;sup × Wbase × Zbase × γconc
216
160
Min. weight of backfill = γG;inf × Wheel × Zheel × γbf;d
660
694.5
Max. weight of backfill = γG;sup × Wheel × Zheel × γbf;d
937.5
694.5
Ka
0.271
0.343
Backfill Force Hap;d = γG;sup × γSd;K × Ka × γbf;d × Z2/2
376
353
Frequent value of Surcharge UDL Force Hsc;udl = ψ1 × γQ × σh;ave × Z
27
29
Frequent value of Surcharge Line Load Force Hsc;F = ψ1 × γQ × Hsc;F
31
33.7
Deck Maximum Permanent load (concrete + surfacingmax) = γG;sup × VDL
273
207
Deck Minimum Permanent load (concrete + surfacingmin) = γG;inf × VDL
172
181
Deck Vertical Traffic load (gr2) = γQ;sup × Vtraffic
120
102
Deck Horizontal Traffic load (gr2) = γQ × Hbraking
49
41
Combination 1
Restoring Effects :
Minimum
V
Lever Arm
Moment About A
Stem
154
1.6
246
Base
152
3.2
486
Backfill
660
4.25
2805
Deck (VDLmin)
172
1.55
267
∑ =
1138
∑ =
3804
Maximum
V
Lever Arm
Moment About A
Stem
219
1.6
350
Base
216
3.2
691
Backfill
937.5
4.25
3984
Deck (VDLmax + Vtraffic)
393
1.55
609
∑ =
1765.5
∑ =
5634
Overturning Effects:
H
Lever Arm
Moment About A
Hap;d
376
3.167
1191
Hsc;udl
27
4.75
128
Hsc;F
31
9.5
295
Hbraking
49
7.5
368
∑ =
483
∑ =
1982
For sliding effects:
φ'cν = 30°
Partial factor on γM on tan(φ'cν;k) = 1.0
Coefficient of friction = μd = tan(φ'cν;k) / γM = tan(30°)/1.0 = 0.58
Sliding resistance = μd∑Vmin = Rνx;d = 0.58 × 1138 = 660kN/m
Active Force = ∑H = 483kN/m < 660 ∴ OK
Bearing Pressure:
EN 1997-1:2004 Cl. 6.5.4 restrict eccentricity of loading to 1/3 of the width of the footing at ULS
V = 1765.5kN/m
Nett moment = 5634 - 1982 = 3652kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (3652 / 1765.5) = 1.131m
Base width / 3 = 6.4 / 3 = 2.131 > 1.131 ∴ OK
Assume rectangular pressure distribution under the base as described in EN 1997-1:2004 Annex D
Effective base width B' = B - 2e = 6.4 - 2 × 1.131 = 4.138m
Pressure under base = (1765.5 / 4.138) = 427kN/m2
R/A' = c'Ncbcscic + q'Nqbqsqiq + 0.5γ'B'Nγbγsγiγ
c' = 0
γ' = γ × γG;inf = 19 × 0.95 = 18.1kN/m3
q' = 1.5 × 18.1 = 27.2kN/m2 (Foundation 1.5m below existing ground level)
Nq = eπtanφ'dtan2(45 + φ'd / 2)
φ'd = φ' = 34° (γM = 1.0)
Nq = eπtan34tan2(45 + 34 / 2) = 29.4
Nγ = 2(Nq - 1)tanφ'd = 2 × (29.4 - 1) × tan34 = 38.3
bq = bγ = 1.0 (α = 0)
B' = 4.138
sq = 1 + (B' / L')sinφ'd = 1 + (4.138 / 11.6) × sin34 = 1.20
sγ = 1 - 0.3(B' / L') = 1 - 0.3(4.138 / 11.6) = 0.89
m = (2 + B' / L') / (1 + B' / L') = (2 + 4.138 / 11.6) / (1 + 4.138 / 11.6) = 1.74
iq = [1 - H / (V + A'c'dcotφ'd)]m = [1 - 483 / 1765.5]1.74 = 0.57
iγ = [1 - H / (V + A'c'dcotφ'd)]m+1 = [1 - 483 / 1765.5]2.74 = 0.42
R/A' = 0 + (27.2 × 29.4 × 1.0 × 1.20 × 0.57) + (0.5 × 18.1 × 4.138 × 38.3 × 1.0 × 0.89 × 0.42 = 547 + 536 = 1083 kN/m2 > 427 kN/m2 ∴ OK.
Combination 2
Restoring Effects :
Minimum
V
Lever Arm
Moment About A
Stem
162.5
1.6
260
Base
160
3.2
512
Backfill
694.5
4.25
2952
Deck (VDLmin)
181
1.55
281
∑ =
1198
∑ =
4005
Maximum
V
Lever Arm
Moment About A
Stem
162.5
1.6
260
Base
160
3.2
512
Backfill
694.5
4.25
2952
Deck (VDLmax + Vtraffic)
309
1.55
479
∑ =
1326
∑ =
4203
Overturning Effects:
H
Lever Arm
Moment About A
Hap;d
353
3.167
1118
Hsc;udl
29
4.75
138
Hsc;F
33.7
9.5
320
Hbraking
41
7.5
308
∑ =
457
∑ =
1884
For sliding effects:
φ'cν = 30°
Partial factor on γM on tan(φ'cν;k) = 1.25
Coefficient of friction = μd = tan(φ'cν;k) / γM = tan(30°)/1.25 = 0.46
Sliding resistance = μd∑Vmin = Rνx;d = 0.46 × 1198 = 551kN/m
Active Force = ∑H = 457kN/m < 551 ∴ OK
Bearing Pressure:
EN 1997-1:2004 Cl. 6.5.4 restrict eccentricity of loading to 1/3 of the width of the footing at ULS
V = 1326kN/m
Nett moment = 4203 - 1884 = 2319kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (2319 / 1326) = 1.451m
Base width / 3 = 6.4 / 3 = 2.131 > 1.451 ∴ OK
Assume rectangular pressure distribution under the base as described in EN 1997-1:2004 Annex D
Effective base width B' = B - 2e = 6.4 - 2 × 1.451 = 3.498m
Pressure under base = (1326 / 3.498) = 379kN/m2
R/A' = c'Ncbcscic + q'Nqbqsqiq + 0.5γ'B'Nγbγsγiγ
c' = 0
γ' = γ × γG;inf = 19 × 1.0 = 19kN/m3
q' = 1.5 × 19 = 28.5kN/m2 (Foundation 1.5m below existing ground level)
Nq = eπtanφ'dtan2(45 + φ'd / 2)
φ'd = tan-1[tan(φ'k)/γM] = tan-1[tan34/1.25] = 28.4°
Nq = eπtan28.4tan2(45 + 28.4 / 2) = 15.4
Nγ = 2(Nq - 1)tanφ'd = 2 × (15.4 - 1) × tan28.4 = 15.6
bq = bγ = 1.0 (α = 0)
B' = 3.498
sq = 1 + (B' / L')sinφ'd = 1 + (3.498 / 11.6) × sin28.4 = 1.14
sγ = 1 - 0.3(B' / L') = 1 - 0.3(3.498 / 11.6) = 0.91
m = (2 + B' / L') / (1 + B' / L') = (2 + 3.498 / 11.6) / (1 + 3.498 / 11.6) = 1.768
iq = [1 - H / (V + A'c'dcotφ'd)]m = [1 - 457 / 1326]1.768 = 0.47
iγ = [1 - H / (V + A'c'dcotφ'd)]m+1 = [1 - 457 / 1326]2.768 = 0.31
R/A' = 0 + (28.5 × 15.4 × 1.0 × 1.14 × 0.47) + (0.5 × 19 × 3.498 × 15.6 × 1.0 × 0.91 × 0.31) = 235 + 146 = 381 kN/m2 > 379 kN/m2 ∴ OK.
Analysing Load Cases 2 to 7 for the fixed abutment and the free abutment using a simple spreadsheet the following results were obtained:
Notation:
Case 2, 6 and 7 - results of fixed abutment with dowels and free abutment with sliding bearings.
Case 2a, 6a and 7a - results of fixed abutment with dowels and free abutment with elastomeric bearings.
Case 2b, 6b and 7b - results of both abutments with elastomeric bearings.
All other cases are not affected by the bearing arrangement.
Fixed Abutment:
Sliding
SLS
Comb.1
Comb.2
Resistance
692
657
553
Case 2
Case 2a
306
375
476
569
453
522
Case 3
290
454
437
Case 4
289
453
436
Case 5
275
435
416
Case 6 & 6a
311
483
458
Case 7& 7a
274
433
402
Bearing
Pressure
SLS
Toe
SLS
Heel
Comb.1
Vd/A' / R/A'
Comb.2
Vd/A' / R/A'
Case 2
Case 2a
359
435
23
-52
384 / 1054
478 / 773
341 / 354
447 / 257
Case 3
393
30
418 / 1199
370 / 426
Case 4
377
36
402 / 1188
354 / 419
Case 5
392
42
418 / 1281
362 / 473
Case 6 & 6a
401
9
427 / 1082
380 / 380
Case 7 & 7a
377
45
403 / 1265
336 / 485
Sliding
SLS
Comb.1
Comb.2
Resistance
692
657
553
Case 2
Case 2a
306
375
476
569
453
522
Case 3
290
454
437
Case 4
289
453
436
Case 5
275
435
416
Case 6 & 6a
311
483
458
Case 7 & 7a
274
433
402
Bearing
Pressure
SLS
Toe
SLS
Heel
Case 2
Case 2a
359
435
23
-52
Case 3
393
30
Case 4
377
36
Case 5
392
42
Case 6 & 6a
401
9
Case 7 & 6a
377
45
Bearing
Pressure
Comb.1
Vd/A' / R/A'
Comb.2
Vd/A' / R/A'
Case 2
Case 2a
384 / 1054
478 / 773
341 / 354
447 / 257
Case 3
418 / 1199
370 / 426
Case 4
402 / 1188
354 / 419
Case 5
418 / 1281
362 / 473
Case 6 & 6a
427 / 1082
380 / 380
Case 7 & 6a
403 / 1265
336 / 485
Free Abutment:
Sliding
SLS
Comb.1
Comb.2
Resistance
711
675
568
Case 2
Case 2a
Case 2b
312
382
339
486
580
522
463
532
490
Case 3
297
465
447
Case 4
269
464
447
Case 5
282
445
426
Case 6 & 6a
Case 6b
282
307
445
479
426
455
Case 7 & 7a
Case 7b
239
260
387
415
363
387
Bearing
Pressure
SLS
Toe
SLS
Heel
Comb.1
Vd/A' / R/A'
Comb.2
Vd/A' / R/A'
Case 2
Case 2a
Case 2b
361
436
390
25
-49
-3
386 / 1070
478 / 793
417 / 957
342 / 360
444 / 262
375 / 320
Case 3
395
31
420 / 1212
371 / 431
Case 4
379
37
404 / 1202
355 / 424
Case 5
394
43
421 / 1294
364 / 477
Case 6 & 6a
Case 6b
364
391
50
23
390 / 1257
416 / 1145
337 / 453
366 / 405
Case 7 & 7a
Case 7b
334
365
92
67
368 / 1480
395 / 1387
300 / 578
326 / 539
Sliding
SLS
Comb.1
Comb.2
Resistance
711
675
568
Case 2
Case 2a
Case 2b
312
382
339
486
580
522
463
532
490
Case 3
297
465
447
Case 4
269
464
447
Case 5
282
445
426
Case 6 & 6a
Case 6b
282
307
445
479
426
455
Case 7 & 7a
Case 7b
239
260
387
415
363
387
Bearing
Pressure
SLS
Toe
SLS
Heel
Case 2
Case 2a
Case 2b
361
436
390
25
-49
-3
Case 3
395
31
Case 4
379
37
Case 5
394
43
Case 6 & 6a
Case 6b
364
391
50
23
Case 7 & 7a
Case 7b
343
365
90
67
Bearing
Pressure
Comb.1
Vd/A' / R/A'
Comb.2
Vd/A' / R/A'
Case 2
Case 2a
Case 2b
386 / 1070
478 / 793
417 / 957
342 / 360
444 / 262
375 / 320
Case 3
420 / 1212
371 / 431
Case 4
404 / 1202
355 / 424
Case 5
421 / 1294
364 / 477
Case 6 & 6a
Case 6b
390 / 1257
416 / 1145
337 / 453
366 / 405
Case 7 & 7a
Case 7b
377 / 1489
395 / 1387
308 / 584
326 / 539
Note:
1) Numbers in bold indicate failed results.
2) Slight differences in results between the example and the spreadsheet for Case 6 are due to rounding off errors in the example.
It can be seen that the use of elastomeric bearings (Case 2) will govern the critical design load cases on the abutments. We shall assume that there are no specific requirements for using elastomeric bearings and design the abutments for the lesser load effects by using sliding bearings.
2) Wall and Base Design
Loads on the back of the wall are calculated using 'at rest' earth pressures. Serviceability and Ultimate load effects need to be calculated for the load cases 2 to 7 shown above. Again, these are best carried out using a simple spreadsheet.
Using the Fixed Abutment Load Case 6 again as an example of the calculations:
Wall Design
SLS
Combination 1
Combination 2
φ'bf;d = tan-1[tan(φ'bf;k)/γM]
35.0°
35.0°
29.3°
K0 = 1-Sinφ'bf;d
0.426
0.426
0.511
Backfill density (γbf;d) = γbf;k γG;sup
19.0
25.7
19.0
Hap;d = γbf;dK0γSd;KZ2/2
4.047Z2kN/m
6.569Z2kN/m
5.825Z2kN/m
Consider a section at the base of the wall (Z = 8.5m)
Backfill:
Hap;d(kN) =
292
475
421
Moment (kNm) (lever arm = 8.5/3) =
827
1295
1193
Frequent value of Normal Surcharge:
ψ1γQ;sup =
0.75
1.013
0.863
ψ1γQ;supHsc;F = ψ1γQ;sup113.79KdDf =
24
33
34
Moment (kNm) (lever arm = 8.5) =
204
281
289
ψ1γQ;supσh;aveZ = ψ1γQ;sup10.34KdZ =
28
38
39
Moment (kNm) (lever arm = 4.25) =
119
162
166
Deck Permanent Load Reaction:
γG;sup for concrete =
1.0
1.35
1.0
Deck concrete =
164
221
164
γG;sup for surfacing =
1.0
1.2
1.0
Deck surfacing =
43
52
43
Moment = Σ V × e (e = 0.5 - 0.45 = 0.05) =
10
14
10
Deck Variable Reaction (gr2):
γQ;sup =
1.0
1.35
1.15
Variable Vertical Reaction =
89
120
102
Moment = V × e (e = 0.5 - 0.45) =
4
6
5
Variable Horizontal Reaction (Braking) =
36
49
41
Moment = H × 6.5 =
234
319
267
Comb.1 shear at base of wall = Σ H = 475 + 33 + 38 + 49 = 595kN
Comb.2 shear at base of wall = Σ H = 421 + 33 + 38 + 41 = 533kN
SLS moment at base of wall = Σ M = 827 + 204 + 119 + 10 + 4 + 234 = 1398kNm (837 permanent + 561 variable)
ULS Comb.1 moment at base of wall = Σ M = 1295 + 281 + 162 + 14 + 6 + 319 = 2077kNm
ULS Comb.2 moment at base of wall = Σ M = 1193 + 289 + 166 + 10 + 5 + 267 = 1930kNm
Analysing the fixed abutment and free abutment with Load Cases 2 to 7 using a simple spreadsheet the following results were obtained for the design moments and shear at the base of the wall:
(Note - Slight differences in results between the example and the spreadsheet for Case 6 are due to rounding off errors in the example.)
Fixed Abutment:
SLS Moment
(Permanent)
SLS Moment
(Variable)
SLS Moment
(Total)
Case 2
840
539
1379
Case 3
840
442
1282
Case 4
840
427
1267
Case 5
840
335
1175
Case 6
840
565
1405
Case 7
840
279
1119
Moment
ULS Comb.1
Shear
ULS Comb.1
Moment
ULS Comb.2
Shear
ULS Comb.2
Case 2
2086
590
1908
534
Case 3
1954
569
1811
518
Case 4
1934
570
1792
519
Case 5
1809
545
1664
494
Case 6
2120
594
1928
535
Case 7
1734
531
1525
469
Free Abutment:
SLS Moment
(Permanent)
SLS Moment
(Variable)
SLS Moment
(Total)
Case 2
878
551
1429
Case 3
878
451
1329
Case 4
878
437
1315
Case 5
878
342
1220
Case 6
878
338
1216
Case 7
878
7
885
Moment
ULS Comb.1
Shear
ULS Comb.1
Moment
ULS Comb.2
Shear
ULS Comb.2
Case 2
2163
606
1979
547
Case 3
2029
584
1880
531
Case 4
2009
585
1860
532
Case 5
1881
560
1729
507
Case 6
1876
560
1724
507
Case 7
1428
489
1266
434
Concrete to BS 8500:2006
Use strength class C32/40 with water-cement ratio 0.5 and minimum cement content of 340kg/m3 for exposure condition XD2.
Nominal cover to reinforcement = 60mm (45mm minimum cover plus a tolerance Δc of 15mm).
Reinforcement to BS 4449:2005 Grade B500B: fy = 500N/mm2
Design for critical moments and shear in Free Abutment:
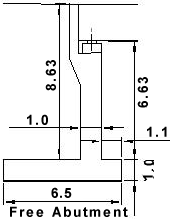
Check slenderness of abutment wall to see if second order effects need to be considered:
EN 1992-1-1 clause 5.8.3.1
λ = 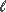 0/i ≤ λlim = 20A.B.C/√n
0/i ≤ λlim = 20A.B.C/√n
Use suggested values when φef not known:
A = 0.7, B = 1.1, C = 0.7
n = NEd / (Acfcd)
NEd = 164 + 43 + 166 = 373kN
fcd = αccfck / γc = 0.85 × 32 / 1.5 = 18.1N/mm2
Ac = 106mm2 (per metre width)
n = 373 × 103 / (106 × 18.1) = 0.021
λlim = 20 × 0.7 × 1.1 × 0.7 / √0.021 = 74.4
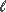 0 = 2 ×
0 = 2 × 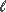 = 2 × 6.63 = 13.26m (cantilever with sliding bearings to deck)
= 2 × 6.63 = 13.26m (cantilever with sliding bearings to deck)
i = √(1/12) = 0.289m
λ = 13.26 / 0.289 = 45.9 < 74.4 ∴ OK, second order effects need not be considered.
EN 1992-1-1 & EN 1992-2
It is usual to design reinforced concrete for the ultimate limit state and check for serviceability conditions.
MULS = 2163kNm/m, VULS = 606kN/m, MSLS = 1429kNm/m [878(permanent)+551(variable)]
cl. 3.1.6(101)P
Design compressive strength = fcd = αccfck / γc
cl. 3.1.7
αcc = 0.85
cl. 2.4.2.4
Table 2.1N: γc = 1.5, γs = 1.15
fcd = 0.85 × 32 / 1.5 = 18.1 N/mm2
Table 3.1
εc2 = 0.002, εcu2 = 0.0035, n = 2.0
Try B40's @ 150mm c/c (8378mm2/m) in rear face at base of wall:
Nominal cover to reinforcement in rear face of wall = 60mm
d = 1000 - 60 - 20 = 920mm
Fig. 3.3
Using parabolic-rectangular diagram:
Average stress fav = fcd[1-εc2 / {εcu2(n+1)}] = 18.1 × [1 - 0.002 / {0.0035 × (2 + 1)}] = 14.7 N/mm2
Assuming steel yields then:
M = fsz = fykAsz / γs = Fcz = favbXz
Depth to neutral axis X = fykAs / (favbγs)
X = 500 × 8378 / (14.7 × 1000 × 1.15) = 247.8mm
Check that steel will yield:
Cl. 3.2.7(4)
Modulus of Elasticity Es = 200 kN/mm2
Steel strain at yield = εs,yield = fyk / γs / Es = 500 / 1.15 / 200000 = 0.00217
from linear strain relationship:
εs = εcu2(d/X - 1) = 0.0035 ( 920 / 247.8 - 1) = 0.009 > 0.00217 ∴ steel will yield.
Hence Mult = favbXz = favbX(d - βX)
Where β = 1 - [0.5εcu22 - εc22 / {(n+1)(n+2)}] / [εcu22 - εcu2εc2 / (n+1)]
β = 1 - [0.5 × 0.00352 - 0.0022 / {(2 + 1) × (2 + 2)}] / 0.00352 - 0.0035 × 0.002 / (2 + 1)] = 0.416
Mult = 14.7 × 1000 × 247.8 × (920 - 0.416 × 247.8) × 10-6 = 2976 kNm > 2163 ∴ OK
Check Serviceability Limit State
Characteristic Combination SLS Design Moment = 1429kNm/m (878 +551)
Check stresses in the concrete and reinforcement at:
i) Early Age (before creep has occurred)
ii) Long term after all the creep has taken place.
i) Before creep has occurred the cracked section properties will be based on the short-term modulus for all actions.
EN 1992-1-1 Table 3.1
Ecm = 22[(fck + 8) / 10]0.3 = 22[(32 + 8) / 10]0.3 = 33.4 kN/mm2
Ec,eff = Ecm = 33.4 kN/mm2
Modular Ratio m = Es / Ecm = 200 / 33.4 = 6.0
Let dc = depth to neutral axis then equating strains for cracked section:
εs = εc(d - dc) / dc
Equating forces:
AsEsεs = 0.5bdcεcEc,eff
Hence dc = [-AsEs + {(AsEs)2 + 2bAsEsEc,effd}0.5] / bEc,eff
dc = [-8378 × 200000 + {(8378 × 200000)2 + 2 × 1000 × 8378 × 200000 × 33400 × 920}0.5] / (1000 × 33400) = 258mm
Cracked second moment of area = As(d-dc)2 + Ec,effbdc3 / 3Es
INA = 8378 × (920 - 258)2 + 33.4 × 1000 × 2583 / (3 × 200) = 4.63 × 109 mm4 (steel units)
Approximate concrete stress σc = M / zc + N / Ac
N (Case 2) = 164 + 43 = 207 kN
σc ≅ {1429 × 106 × 258 / (4.63 × 109 × 6.0)} + {207 × 103 / (258 × 103)} = 13.3 + 0.8 = 14.1 N/mm2
cl. 7.2(102)
Limiting concrete stress = k1fck
k1 = 0.6
Limiting concrete stress = 0.6 × 32 = 19.2 N/mm2 > 14.1 ∴ OK
EN 1992-1-1
ii) After all creep has taken place the cracked section properties will be based on the long-term and short-term modulus for the various actions.
Short-term modulus = Ecm
Long-term modulus = Ecm / (1+φ)
Effective modulus Ec,eff = (Mqp + Mst)Ecm / {Mst + (1 + φ)Mqp}
Table 3.1
fcm = fck + 8 = 32 + 8 = 40 N/mm2
Cl. 3.1.4
Relative humidity of the ambient environment = 80% (outside conditions)
Age of concrete at initial loading t0 = say 7 days (after formwork has been released and waterproofing system applied to rear face of wall)
Annex B (B.6)&(B.8c)
h0 = 2Ac / U = 2 × (11600 × 1000) / (11600 + 2 × 1000) = 1706
α1 = [35 / fcm]0.7 = [35 / 40]0.7 = 0.91
α2 = [35 / fcm]0.2 = [35 / 40]0.2 = 0.97
(B.3b)
φRH = [1 + α1 × {(1 - RH / 100) / (0.1 × h01/3)}] × α2
φRH = [1 + 0.91 × {(1 - 80 / 100) / ( 0.1 × 17061/3)}] × 0.97 = 1.118
(B.4)
β(fcm) = 16.8 / fcm0.5 = 16.8 / 400.5 = 2.656
(B.5)
β(t0) = 1 / (0.1 + t00.2) = 1 / ( 0.1 + 70.2) = 0.635
(B.2)
φ0 = φRH × β(fcm) × β(t0) = 1.118 × 2.656 × 0.635 = 1.886
Moment due to long-term actions = Mqp = 878 kNm
Moment due to short-term actions = Mst = 551 kNm
Hence Effective Modulus Ec,eff = {(878 + 551) × 33.4} / {551 + 878 × ( 1 + 1.886)} = 15.5 kN/mm2
Modular Ratio m = Es / Ec,eff = 200 / 15.5 = 12.9
Let dc = depth to neutral axis then equating strains for cracked section:
εs = εc(d - dc) / dc
Equating forces:
AsEsεs = 0.5bdcεcEc,eff
Hence dc = [-AsEs + {(AsEs)2 + 2bAsEsEc,effd}0.5] / bEc,eff
dc = [-8378 × 200000 + {(8378 × 200000)2 + 2 × 1000 × 8378 × 200000 × 15500 × 920}0.5] / (1000 × 15500) = 351mm
Cracked second moment of area = As(d-dc)2 + Ec,effbdc3 / 3Es
INA = 8378 × (920 - 351)2 + 15.5 × 1000 × 3513 / (3 × 200) = 3.83 × 109 mm4 (steel units)
Concrete stress σc ≅ M / zc + N / Ac
σc = {1429 × 106 × 351 / (3.83 × 109 × 12.9)} + (207 × 103 / (351 × 103) = 10.2 + 0.6 = 10.8 N/mm2
cl. 7.2(102)
Limiting concrete stress = k1fck
k1 = 0.6
Limiting concrete stress = 0.6 × 32 = 19.2 N/mm2 > 10.8 ∴ OK
cl. 7.2(5)
Limiting steel stress = k3fyk
k3 = 0.8
Limiting steel stress = 0.8 × 500 = 400 N/mm2
Steel stress σs = M / zs
σs = 1429 × 106 × (920 - 351) / (3.83 × 109) = 212 N/mm2 < 400 ∴ >OK
Crack Control:
Consider worst condition before creep has occurred and
Quasi-Permanent Combination Moment + ψ2 × temperature effects = 878 + 0.5(16 × 6.63) = 931 kNm
Cl. 7.3.4(1)
Crack width wk = sr,max(εsm - εcm)
Cl. 7.3.4(3)
Spacing Limit = 5(c+φ/2) = 5(60 + 40/2) = 400mm > 150mm ∴ OK
sr,max = k3c + k1k2k4φ / ρp,eff
k1 = 0.8 (high bond bars)
k2 = 0.5 (for bending)
k3 = 3.4 (recommended value)
k4 = 0.425 (recommended value)
Cl. 7.3.2(3)
hc,eff is the lesser of:
i) 2.5(h-d) = 2.5(1000 - 920) = 200
ii) (h-x)/3 = (1000 - 258) / 3 = 247
iii) h/2 = 1000 / 2 = 500
∴ hc,eff = 200 mm
and Ac,eff = 200 × 1000 = 200000 mm2
Cl. 7.3.4(2)
ρp,eff = As / Ac,eff = 8378 / 200000 = 0.0419
sr,max = k3c + k1k2k4φ / ρp,eff
sr,max = (3.4 × 60) + (0.8 × 0.5 × 0.425 × 40) / 0.0419 = 204 + 162 = 366
Cl. 7.3.4(2)
(εsm - εcm) = [σs - {ktfct,eff(1 + αeρp,eff) /ρp,eff}] / Es ≥ 0.6σs / Es
kt = 0.4 for permanent loading
αe = Es / Ecm = 200 / 33.4 = 6.0
σs = 931 × 106 × (920 - 258) / (4.63 × 109) = 133 N/mm2
Table 3.1
fct,eff = fctm = 0.3 × fck(2/3) = 0.3 × 32(2/3) = 3.02 N/mm2
(εsm - εcm) = [133 - {0.4 × 3.02 × (1 + 6.0 × 0.0419) / 0.0419}] / 200000 = 0.485 × 10-3
0.6σs / Es = 0.6 × 133 / 200000 = 0.399 × 10-3 < 0.485 × 10-3 ∴ OK
Crack width wk = sr,max(εsm - εcm) = 366 × 0.485 × 10-3 = 0.18 mm
NA EN 1992-2 Table NA.2
Recommended value of wmax = 0.3 mm > 0.18 mm ∴ OK
Hence B40 bars at 150 centres are adequate for the rear face at the base of the wall.
Shear Capacity
Cl. 6.2.2(101)
Shear Capacity of Wall with B40 dia. reinforcement @ 150c/c
VRd,c = [CRd,ck(100ρ1fck)1/3]bwd
CRd,c = 0.18 / γc = 0.18 / 1.5 = 0.12
k = 1 + (200 / d)0.5 ≤2.0
k = 1 + (200 / 920)0.5 = 1.47 < 2.0
ρ1 = Asl / bwd ≤0.02
ρ1 = 8378 / (1000 × 920) = 0.009 < 0.02
Cl. 3.1.2(102)P
fck = 32 ( < Cmax = C50/60)
VRd,c = [0.12 × 1.47 × (100 × 0.009 × 32)1/3] × 1000 × 920 × 10-3 = 497 kN ( < 606 kN Fail : see below)
Minimum VRd,c = (vmin)bwd = 0.035k3/2fck1/2bwd = 0.035 × 1.473/2 × 321/2 × 1000 × 920 × 10-3 = 325 kN
cl 6.2.2(6)
Check that the maximum allowable shear force is not exceeded:
Maximum allowable shear force = 0.5bwdνfcd
ν = 0.6[1 - fck / 250] = 0.6 × [1 - 32 / 250] = 0.523
fcd = αccfck/γc
αcc = 1.0 [see NA to Cl. 3.1.6(101)P]
fcd = 1.0 × 32 / 1.5 = 21.3 N/mm2
Maximu VEd = 0.5 × 1000 × 920 × 0.523 × 21.3 × 10-3 = 5124 kN >> 606 kN
VRd,c = 497 kN < VEd = 606 kN ∴ Fail. It would be necessary to increase the longitudinal reinforcement to B40 at 125 c/c however the UK National Annex allows an alternative approach.
NA to 1992-2 Cl. 6.2.2(101)
Alternative Solution:
If the reduction factor β is not used to reduce the applied shear force actions then the allowable shear force VRd,c may be enhanced if the section being considered is within 2d of the support.
i) Consider a section at (a = 0.829m) from the bottom of wall :
Maximum ULS shear force from spreadsheet for Case 2 = 511 kN
Shear enhancement factor = (2d/a) = 2 × 0.92 / 0.829 = 2.22
VRd,c = 2.22 × 497 = 1103 kN ( > 511 kN ∴ OK)
ii) Consider a section at (a = 1.657m) from the bottom of wall :
Maximum ULS shear force from spreadsheet for Case 2 = 426 kN
Shear enhancement factor = (2d/a) = 2 × 0.92 / 1.657 = 1.11
VRd,c with no enhancement = 497 kN > 426 kN ∴, by inspection, all sections will be suitable to resist shear using B40 bars at 150 centres.
Early Thermal Cracking
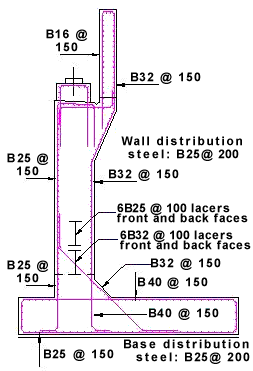
Considering the effects of casting the wall stem onto the base slab by complying with the early thermal cracking of concrete to C660 then B32 horizontal lacer bars @ 100 c/c will be required in both faces in the bottom 0.5m of the wall, reducing to B25 bars @ 200 above 1.3m from the bottom of the wall.
Minimum Wall Reinforcement
EN 1992-1-1 Clause 9.6.2 - Vertical reinforcement:
As,vmin = 0.002Ac = 0.002 × 106 = 2000 mm2/m (1000 mm2/m in each face). Use B16 @ 150 c/c (As = 1340mm2/m).
EN 1992-1-1 Clause 9.6.3 - Horizontal reinforcement:
As,vmin = 0.001Ac or 25% of vertical reinforcement = 0.001 × 106 = 1000 mm2/m (in each face) or
25% × 8378 = 2095mm2/m. B20 @ 150 c/c = 2094mm2/m, but B32 @ 100 c/c reducing to B25 bars @ 150 are required to resist early thermal cracking.
Hence early thermal cracking and long-term creep and shrinkage crack control require greater areas of reinforcement than the minimum wall reinforcement.
Base Design
Maximum bending and shear effects in the base slab will occur at sections near the front and back of the wall. Calculations need to be carried out for serviceability and ultimate limit states using 'at rest pressures'
Using the Fixed Abutment Load Case 6 again as an example of the calculations:
CASE 6 - Fixed Abutment Serviceability Limit State

Weight of wall stem = 162.5kN/m
Weight of base = 160kN/m
Weight of backfill = 694.5kN/m
B/fill Force Hap;d = γG × γSd;K × K0 × γbf;d × Z2 / 2 = 1.0 × 1.0 × 0.426 × 19 × 9.52 / 2 = 365kN/m
Frequent value of Surcharge UDL Force Hsc;udl = ψ1 × γQ × σh;ave × Z = 0.75 × 1.0 × (10.34 × 0.426) × 9.5 = 31kN/m
Dispersion Factor Df for line load = (1 + Z / 2) / (1 + Z) = (1 + 9.5 / 2) / (1 + 9.5) = 0.55 < 0.67 ∴ Df = 0.67
Frequent value of Surcharge Line Load Force Hsc;F = ψ1 × γQ × Hsc;F = 0.75 × 1.0 × (113.79 × 0.426 × 0.67) = 24kN/m
Deck Maximum Permanent load (concrete + surfacingmax) = 207kN/m
Deck Vertical Traffic load (gr2) = 89kN/m
Deck Horizontal Traffic load (gr2) = 36kN/m
Restoring Effects:
V
Lever Arm
Moment About A
Stem
162.5
1.6
260
Base
160
3.2
512
Backfill
694.5
4.25
2952
Deck Vertical Reaction
296
1.55
459
∑ =
1313
∑ =
4183
Overturning Effects:
H
Lever Arm
Moment About A
Backfill
365
3.167
1156
Surcharge UDL
31
4.75
147
Surcharge Line Load
24
9.5
228
Deck Horizontal Reaction
36
7.5
270
∑ =
456
∑ =
1801
Bearing Pressure at toe and heel of base slab = (V / A) ± (V × e × y / I)
V = 1313kN/m
A = 6.4m2/m
I / y = 6.42 / 6 = 6.827m3/m
Nett moment = 4183 - 1801 = 2382kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (2382 / 1313) = 1.386m
Pressure under base = (1313 / 6.4) ± (1313 × 1.386 / 6.827)
Pressure under toe = 205 + 267 = 472kN/m2
Pressure under heel = 205 - 267 = -62kN/m2 (uplift)
Adjust for uplift:
Reduced length of pressure under base = 3(B/2 - e) = 3 × (6.4 / 2 - 1.386) = 5.442 m
Pressure under toe = 2 × 1313 / 5.442 = 483 kN/m2
Pressure at front face of wall = 483 × 4.342 / 5.442} = 385kN/m2
Pressure at rear face of wall = 483 × 3.342 / 5.442} = 297kN/m2
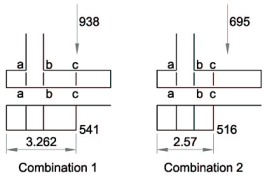
SLS Moment at a-a = (385 × 1.12 / 2) + ([483 - 385] × 1.12 / 3) - (25 × 1.0 × 1.12 / 2) = 257kNm/m (tension in bottom face).
SLS Moment at b-b = (297 × 3.3422 / 6) - (695 × 4.3 / 2) - (25 × 1.0 × 4.32 / 2) = -1173kNm/m (tension in top face).
CASE 6 - Fixed Abutment Ultimate Limit State

Weight of wall stem Comb.1 = γG;sup × 162.5 = 1.35 × 162.5 = 219 kN/m
Weight of wall stem Comb.2 = γG;sup × 162.5 = 1.0 × 162.5 = 163 kN/m
Weight of base Comb.1 = γG;sup × 160 = 1.35 × 160 = 216 kN/m
Weight of base Comb.2 = γG;sup × 160 = 1.0 × 160 = 160 kN/m
Weight of backfill Comb.1 = γG;sup × 694.5 = 1.35 × 694.5 = 938 kN/m
Weight of backfill Comb.2 = γG;sup × 694.5 = 1.0 × 694.5 = 695 kN/m
B/fill Force Hap;d Comb.1 = γG;sup × γSd;K × K0 × γbf;d × Z2 / 2 = 1.35 × 1.2 × 0.426 × 19 × 9.52 / 2 = 592kN/m
B/fill Force Hap;d Comb.2 = γG;sup × γSd;K × K0 × γbf;d × Z2 / 2 = 1.0 × 1.2 × 0.511 × 19 × 9.52 / 2 = 526kN/m
Frequent value of Surcharge UDL Force Hsc;udl Comb.1 = ψ1 × γQ;sup × σh;ave × Z = 0.75 × 1.35 × (10.34 × 0.426) × 9.5 = 42kN/m
Frequent value of Surcharge UDL Force Hsc;udl Comb.2 = ψ1 × γQ;sup × σh;ave × Z = 0.75 × 1.15 × (10.34 × 0.511) × 9.5 = 43kN/m
Dispersion Factor Df for line load = (1 + Z / 2) / (1 + Z) = (1 + 9.5 / 2) / (1 + 9.5) = 0.55 < 0.67 ∴ Df = 0.67
Frequent value of Surcharge Line Load Force Hsc;F Comb.1 = ψ1 × γQ;sup × Hsc;F = 0.75 × 1.35 × (113.79 × 0.426 × 0.67) = 33kN/m
Frequent value of Surcharge Line Load Force Hsc;F Comb.2 = ψ1 × γQ;sup × Hsc;F = 0.75 × 1.15 × (113.79 × 0.511 × 0.67) = 34kN/m
Deck Maximum Permanent load (concrete + surfacingmax) Comb.1 = γG;sup × 164 + γG;sup × 43 = 1.35 × 164 + 1.2 × 43 = 273kN/m
Deck Maximum Permanent load (concrete + surfacingmax) Comb.2 = γG;sup × 164 + γG;sup × 43 = 1.0 × 164 + 1.0 × 43 = 207kN/m
Deck Vertical Traffic load (gr2) Comb.1 = γQ;sup × 89 = 1.35 × 89 = 120 kN/m
Deck Vertical Traffic load (gr2) Comb.2 = γQ;sup × 89 = 1.15 × 89 = 102 kN/m
Deck Horizontal Traffic load (gr2) Comb.1 = γQ;sup × 36 = 1.35 × 36 = 49 kN/m
Deck Horizontal Traffic load (gr2) Comb.2 = γQ;sup × 36 = 1.15 × 36 = 41 kN/m
Restoring Effects:
V
Comb.1/Comb.2
Lever Arm
Moment About A
Comb.1/Comb.2
Stem
219/163
1.6
350/261
Base
216/160
3.2
691/512
Backfill
938/695
4.25
3987/2954
Deck Vertical Reaction
393/309
1.55
609/479
∑ =
1766/1327
∑ =
5637/4206
Overturning Effects:
H
Lever Arm
Moment About A
Backfill
592/526
3.167
1875/1666
Surcharge UDL
42/43
4.75
200/204
Surcharge Line Load
33/34
9.5
314/323
Deck Horizontal Load
49/41
7.5
368/308
∑ =
716/644
∑ =
2757/2501
Assume rectangular pressure distribution under the base as described in EN 1997-1:2004 Annex D
Combination 1:
V = 1766 kN/m
Nett moment = 5637 - 2757 = 2880 kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (2880 / 1766) = 1.569m
Effective base width B' = B - 2e = 6.4 - 2 × 1.569 = 3.262m
Pressure under base = (1766 / 3.262) = 541 kN/m2
Combination 2:
V = 1327 kN/m
Nett moment = 4206 - 2501 = 1705 kNm/m
Eccentricity (e) of V about centre-line of base = 3.2 - (1705 / 1327) = 1.915m
Effective base width B' = B - 2e = 6.4 - 2 × 1.915 = 2.57m
Pressure under base = (1327 / 2.57) = 516 kN/m2
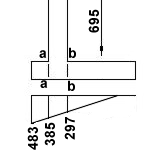
Combination 1:
ULS Shear at a-a = (541 × 1.1) - (1.35 × 1.0 × 1.1 × 25) = 558 kN/m
ULS Shear at b-b = 541 × (3.262 - 2.1) - (1.35 × 1.0 × 4.3 × 25) - 938} = -454 kN/m
ULS Shear at c-c = 1.35 × (6.4 - 3.262) × (8.5 × 19 + 1.0 × 25) = 790 kN/m
ULS Moment at a-a = (541 × 1.12 / 2) - (1.35 × 25 × 1.0 × 1.12 / 2) = 307 kNm/m (tension in bottom face).
ULS Moment at b-b = (541 × (3.262 - 2.1)2 / 2) - (1.35 × 25 × 1.0 × 4.32 / 2) - (938 × 4.3 / 2) = -1963 kNm/m (tension in top face).
Combination 2:
ULS Shear at a-a = (516 × 1.1) - (1.0 × 1.0 × 1.1 × 25) = 540 kN/m
ULS Shear at b-b = 516 × (2.57 - 2.1) - (1.0 × 1.0 × 4.3 × 25) - 695} = 560 kN/m
ULS Shear at c-c = 1.0 × (6.4 - 2.57) × (8.5 × 19 + 1.0 × 25) = 714 kN/m
ULS Moment at a-a = (516 × 1.12 / 2) - (1.0 × 25 × 1.0 × 1.12 / 2) = 297 kNm/m (tension in bottom face).
ULS Moment at b-b = (516 × (2.57 - 2.1)2 / 2) - (1.0 × 25 × 1.0 × 4.32 / 2) - (695 × 4.3 / 2) = -1668 kNm/m (tension in top face).
Analysing the fixed abutment and the free abutment with Load Cases 2 to 7 using a simple spreadsheet the following results were obtained:
Fixed Abutment Base:
Section a-a
ULS Shear
Comb.1/Comb.2
SLS
Moment
ULS Moment
Comb.1/Comb.2
Case 2
509/501
235
280/276
Case 3
539/515
253
297/283
Case 4
521/497
244
286/273
Case 5
527485
250
290/267
Case 6
558/541
258
307/298
Case 7
445/433
235
272/238
Section b-b
ULS Shear
Comb.1/Comb.2
SLS
Moment
ULS Moment
Comb.1/Comb.2
Case 2
480/588
1184
1962/1676
Case 3
364/466
1071
1835/1610
Case 4
372/468
1069
1830/1607
Case 5
290/365
973
1716/1519
Case 6
453/561
1178
1961/1668
Case 7
281/311
934
1663/1436
Section c-c
ULS Shear
Comb.1/Comb.2
Case 2
777/718
Case 3
737/675
Case 4
730/671
Case 5
694/627
Case 6
790/715
Case 7
665/583
Free Abutment Base:
Section a-a
ULS Shear
Comb.1/Comb.2
SLS
Moment
ULS Moment
Comb.1/Comb.2
Case 2
511/500
236
281/275
Case 3
542/516
254
298/284
Case 4
523/498
246
288/274
Case 5
530/487
251
292/268
Case 6
494/455
234
272/250
Case 7
440/372
212
242/205
Section b-b
ULS Shear
Comb.1/Comb.2
SLS
Moment
ULS Moment
Comb.1/Comb.2
Case 2
479/582
1239
2054/1765
Case 3
365/464
1124
1924/1693
Case 4
373/467
1122
1918/1690
Case 5
291/365
1023
1800/1597
Case 6
327/394
1040
1815/1611
Case 7
172/192
741
1428/1266
Section c-c
ULS Shear
Comb.1/Comb.2
Case 2
793/733
Case 3
755/691
Case 4
747/687
Case 5
711/643
Case 6
702/643
Case 7
563/499
Early Thermal Cracking
Considering the effects of casting the base slab onto the blinding concrete by complying with the early thermal cracking of concrete to C660 then a minimum steel area of B25 distribution bars @ 200 c/c will be required to comply with clause 7.3.2(2) of BS EN 1992-1-1.
Design for bending effects at section a-a for the Fixed Abutment and b-b for the Free Abutment and for shear at section c-c for the Free Abutment using a simple spreadsheet for slab member capacities:
Section a-a: Muls = 307 kNm/m, Vuls = 558 kN/m, Msls = 258 kNm/m (Mperm = 181 kNm/m + Mvar = 77 kNm/m)
B25's @ 150 c/c give Muls = 1262 kNm/m > 307 ∴ OK, Vuls = 731 kN/m (at d from support) > 558 ∴ OK, Msls = 1103 kNm/m > 258 ∴ OK
Section b-b: Muls = 2054 kNm/m, Vuls = 582 kN/m, Msls = 1239 kNm/m (Mperm = 860 kNm/m + Mvar = 380 kNm/m)
B40's @ 150 c/c give Muls = 2975 kNm/m > 2054 ∴ OK, Vuls = 996 kN/m (at d from support) > 582 ∴ OK, Msls = 2065 kNm/m > 1239 ∴ OK
Section c-c: Vuls = 793 kN/m < Vuls = 996 kN/m (at d from support using B40's @ 150 c/c) ∴ OK
Local Effects
Curtain Wall (Abutment Upstand Wall)
This wall is designed to be cast onto the top of the abutment after the deck has been built. Loading will be applied from the backfill, surcharge and braking loads on top of the wall.
EN 1991-2 Clause 4.9.2(2):
Braking Force = 0.6αQ1Q1k from LM1 axle = 0.6 × 300 = 180kN
To allow for load distribution effects assume a 45° dispersal down the wall, with maximum dispersal of the width of the abutment (11.6m). Positioning the axle in the centre of the 3.0m notional lane gives a distribution width of 7.65m at the base of the wall.
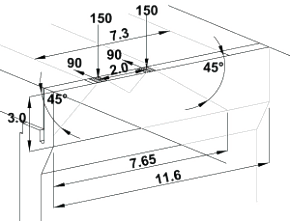
Shear at the base of the wall:
due to braking = 180 / 7.65 = 23.5kN/m
due to backfill = K0 γbf;d Z2 / 2 = 0.426 × 19.0 × 3.02 / 2 = 36kN/m
Total ULS shear = 1.35 × (23.5 + 1.2 × 36) = 90kN/m
Bending moment at the base of the wall:
due to braking = 180 × 3.0 / 7.65 = 70.6kNm/m
due to backfill = K0 γbf;d Z3 / 6 = 0.426 × 19.0 × 3.03 / 6 = 36kNm/m
Total SLS moment = 70.6 + 36 = 107kNm/m
Total ULS moment (combination 1) = (1.35 × 70.6) + (1.35 × 1.2 × 36) = 154kNm/m
Check effects of surcharge + backfill at base of curtain wall:
Normal traffic surcharge:
Df = (1 + Z/2) / (1 + Z) = (1 + 3/2) / (1 + 3) = 0.625 < 0.67 ∴ Df = 0.67
Line Load = 2/3 × 330 KdDf = 220 × 0.426 × 0.67 = 62.8kN/m
UDL = 20Kd = 20 × 0.426 = 8.5kN/m2
Total ULS shear = 1.35 × (62.8 + 8.5 × 3.0 + 1.2 × 36) = 178kN/m
Total SLS moment = 62.8 × 3.0 + 8.5 × 3.02 / 2 + 36 = 188.4 + 38.3 + 36 = 263kNm/m
Total ULS moment = 1.35 × (188.4 + 38.3) + (1.35 × 1.2 × 36) = 306 + 58 = 364kNm/m
SV/196 traffic surcharge:
Line Load = 2/3 × 330 KdDf = 220 × 0.426 × 0.67 = 62.8kN/m
UDL = 30Kd = 30 × 0.426 = 12.8kN/m2
Total ULS shear = 1.35 × (62.8 + 12.8 × 3.0 + 1.2 × 36) = 195kN/m
Total SLS moment = 62.8 × 3.0 + 12.8 × 3.02 / 2 + 36 = 188.4 + 57.6 + 36 = 282kNm/m
Total ULS moment = 1.35 × (188.4 + 57.6) + (1.35 × 1.2 × 36) = 332 + 58 = 390kNm/m
Hence SV/196 Traffic Surcharge + Backfill has worst effect on curtain wall.
400 thick curtain wall with B32 @ 150 c/c :
Mult = 601 kNm/m > 390 kNm/m ∴ OK
Msls = 317 kNm/m > 282 kNm/m ∴ OK
Vult = 261 kN/m > 195 kN/m ∴ Shear OK
Contact David Childs