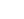Buried Box Design to BD 31 (BS 5400 Standard)
Index
1. Materials & Construction
Departmental Standard BD 31 Chapter 5 gives the requirements for the materials and construction for buried concrete box structures. These structures include in-situ or precast culverts and underpasses.
The construction of the box structure will have implications on the design which need to be considered.
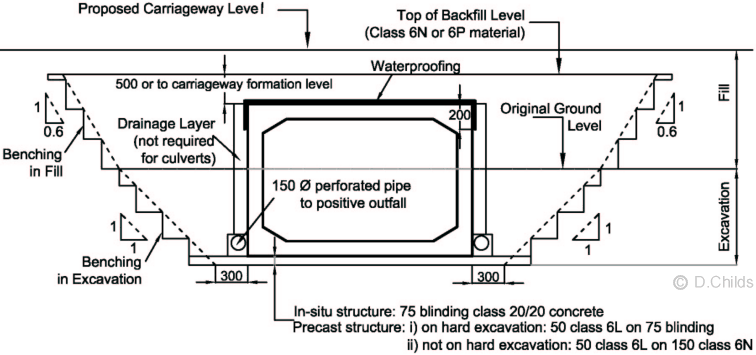
Although vertical drainage layers are required to be provided for underpasses ground water levels and the possibility of buoyancy effects needs to be considered as described in load case diagram A/7a. The drainage layer separates the backfill soil from the walls of the box however the back of wall friction is deemed to be included in the tabulated coefficients in the diagrams/tables.
Preparation of the foundation for the box is important to ensure the structure is evenly supported. The definition of the existing ground material below the box is either 'hard' or 'not hard'; 'hard material' being defined as material which requires the use of blasting, breakers or splitters for its removal. The diagram above shows how either blinding concrete or granular material needs to be placed below the structure to achieve a uniform bedding layer.
Backfill to the structure is restricted to Class 6N or 6P material as defined in the Manual of Contract Documents for Highway Works Volume 1 Specification Series 600 Clause 610 and Table 6/1.
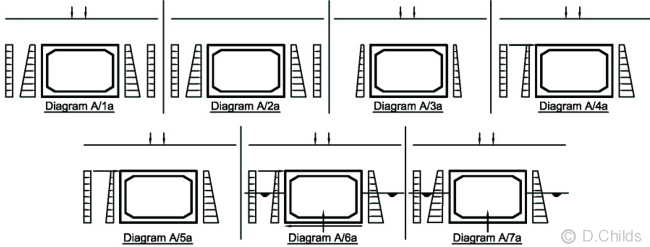
Coefficients of earth pressure for Class 6N and 6P material used in diagrams A/1a to A/7a are:
Ka = 0.33 which equates to a ϕ' value of 30°
Ko = 0.6 which equates to a ϕ' value of 23.6°
In diagram A/6a a limitation for Kr is given as 1.5 or 0.5Kp which again equates to a ϕ' value of 30°
In diagram A/3a a minimum value for K is given as 0.2 to consider the minimum earth pressure effects when the roof structure is heavily loaded with traffic.
For in-situ concrete structures the Standard recommends that longitudinal joints (see 'Dimension Notation' diagram below) are avoided (see clause 4.2.4(c))
2. Loading
Permanent loading comprises of the self-weight of the box, the weight of the carriageway construction and fill over the box, horizontal earth pressures from the backfill material, hydrostatic pressures from ground water, and settlement.
Both the minimum and maximum values of permanent loads need to be considered to assess the worst effects in the structure. The weight of the material over the box acting on the roof slab can be enhanced by the effect of negative arching.
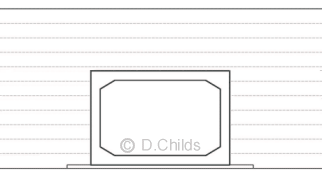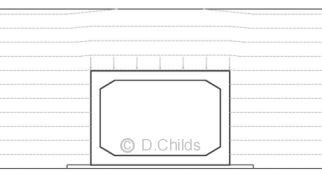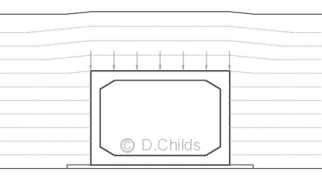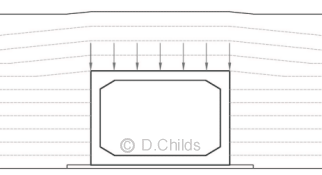
Negative Arching
Negative arching effects are caused by consolidation or settlement of the fill either side of the structure. This effect increases the load from the fill over the roof slab by a factor of β. Values of β are given in Figure 3.1 and are shown to increase linearly above a fill depth of 8m up to 11m. The scope of the Standard limits designs up to a maximum of 11m fill depth above the roof slab.
Horizontal earth pressures can vary considerably, the range of values for the earth pressure coefficients, together with appropriate combination load factors are shown in the tables below Diagrams A/1a to A/7a in Appendix A.
Live Loads consist of traffic loading (HA and HB for BD 31, or LM1, LM2 and LM3 for PD 6694), footway loading, accidental wheel loading, construction traffic, traction and skidding loads, parapet collision loads, centrifugal loads and temperature effects. Although the list is extensive all the items need to be considered, however some may be discounted by observation.
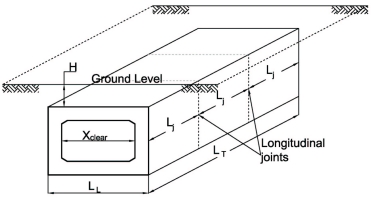
Dimension Notation
Temperature effects may be neglected when:
(i) Cover H > 2m and Xclear < 0.2LT
or
(ii) Overall length LL≤3m.
If the cover H is greater than 0.6m then skidding, centrifugal and HA traction loads may be neglected. HB traction loads may be neglected when cover H ≥ overall length LL.
Note: the scope of the Standard limits designs to structures with the length between the inside faces of the outermost walls (Xclear for single cell) of between 0.9m and 15.0m.
When cover H is 0.6m or less than three vertical live loads need to be considered:
- 100kN HA wheel load.
A load dispersal of 2 vertical to 1 horizontal from the edge of the patch load is permitted through the fill. The size of a square patch load to produce an effective pressure of 1.1N/mm2 = √(100000/1.1) = 302 × 302mm. - HA UDL and KEL loading.
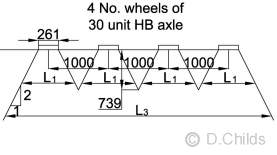
There is no dispersal allowed for either the UDL or KEL so for a 3.65m carriageway width the nominal UDL = 336(1/L)0.67 kN/m and KEL = 120 kN. - A minimum of 30 units HB vehicle (45 units for Trunk Roads and Motorways).
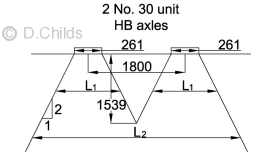
A 2:1 dispersal is permitted as described in (i) above. The wheel load for a 30 unit HB vehicle = 300/4 = 75kN. This will produce a square patch load of 261 × 261mm.
Similarly a 45 unit HB vehicle will produce a wheel patch load of 320 × 320mm on the carriageway.
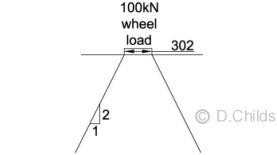
100kN wheel load dispersal
30 unit HB wheel load transverse dispersal
30 unit HB wheel load longitudinal dispersal
When cover H is greater than 0.6m then the HA UDL and KEL loading does not adequately model traffic loading so live loading is restricted to the 100kN wheel load and a minimum of 30 units of HB vehicle.
When cover H is greater than 0.74m then the wheel load dispersal lines for the 30 unit HB axle will overlap and the total axle load is applied to the dispersed width L3.
When cover H is greater than 1.54m then the wheel load dispersal lines for the 30 unit HB front two or rear two axles will overlap and the total bogie load is applied to the dispersed length L2.
If the dispersal lines intersect headwalls before they reach the roof of the structure then the dispersal length (L1, L2 or L3) needs to be reduced appropriately.
If there are no longitudinal joints in the structure then the Standard allows the dispersal lines to continue through the roof slab down to its neutral axis at an angle of 45°. The depth to the neutral axis may be taken as half the depth of the roof slab.
Live load surcharge represents vehicles positioned adjacent to the box structure and is applied as a uniformly distributed load to the side of the box. The UDL is determined by multiplying a vertical UDL by the appropriate earth pressure coefficient listed in Diagrams A/1a to A/7a. The vertical UDLs associated with the various types of live loading are listed in Clause 3.2.6(a).
The UDL surcharge load is applied in conjunction with the vertical live load vehicle over the roof slab in Diagrams A/1a, and A/4a to A/7a. The magnitude of the surcharge relates to the vertical live load vehicle over the box and does not represent the associated HA UDL in the case of an HB vehicle. Diagram A/2a represents the case with surcharge applied to the sides of the box with no vertical live load over the box, whilst Diagram A/3a has no surcharge but vertical live load over the roof only.
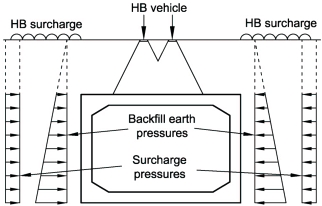
Example of HB live loading
Load Case Combinations to be considered:
Temperature effects need to be considered when the depth of fill over the structure is shallow, or when the maximum clear span is more than 20% of the width LT of the structure. The two effects that need to be analysed are:
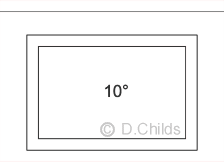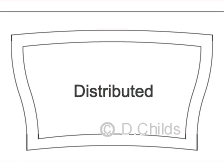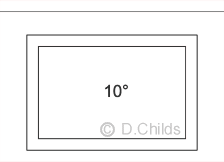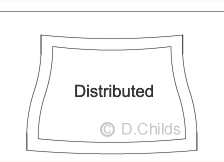
- Temperature Range.
This is the expansion and contraction effect of the roof slab. A mid-range temperature of 10° is assumed with expansion up to Tmax and contraction down to Tmin. Tmax and Tmin are obtained from Table 3.1 of BD 31/01 and are dependent on the depth of cover and dimensions of the structure.
Temperature Range Effects - Differential Temperature.
This occurs when there is a temperature gradient through the roof slab, i.e. when there is a different temperature on the top of the slab to that on the soffit. BD 37/01 Clause 5.4.5 is used to determine the effects of temperature difference. Self equilibrating stresses may be ignored, unless the roof slab is prestressed, however the restraining moments and forces need to be distributed into the structure. A reduction factor η is applied to temperature difference effects to reflect the depth of fill over the roof slab.
There is a simplified method on Appendix C of BD 31/01 for determining the moments and shears around the structure.
3. Stability
Stability of the box is considered in Diagrams A/4a to A/7a where horizontal live loads, such as traction forces, are applied to one side of the box. Stability is maintained by either increasing the horizontal earth pressures on the opposite side of the box, or considering friction forces on the base of the box, or a combination of the two effects.
Sliding effects are considered in Diagram A/6a. The out-of-balance horizontal force is resisted by friction under the base of the box and passive resistance of the soil on the side of the box. A limit of 0.5Kp has been applied for the soil pressure on the passive side of the box. The forces in Diagram A/6a are considered at Ultimate Limit State only.
Bearing pressures are assessed in Diagram A/7a and are considered at Serviceability Limit State only.
Allowable bearing pressures are obtained from the Ground Investigation Survey. An allowable pressure is usually determined to limit differential settlement to about 20 to 25mm.
4.Analysis
A simple unit strip method of analysis is usually suitable for most box designs. Where the fill over the structure is shallow then the 2:1 wheel load dispersal described above will be small and a unit strip method will not model the transverse distribution of the load in the roof slab. In these cases it may prove more economical to analyse the structure using a 3D model.
A simple plane frame model will usually be suitable for modelling the distribution effects of the loads around the structure. Alternatively a moment distribution analysis can be used effectively.
Moments and shears are determined at critical points around the structure, i.e at corners and mid lengths of walls, roof and floor slabs. The critical section for shear in the slabs is at distance d from the end of the splay, or the corner when there is no splay, as shown.
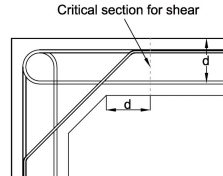
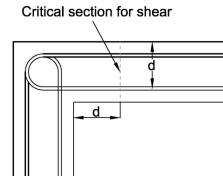
It is important to check for combined bending and shear at these critical sections.
Special attention to reinforcement detailing is required when bending causes tension on the inside of the box at the corners. Appendix D of the Standard describes a method of designing for these corner 'opening' moments. An example of the calculation has been provided in the Workshop Section of this website.
Design Example to BD 31 | Back to Tutorial Index
Contact David Childs